Pythagoras' Theorem

Session 1

In this session students explore squares numbers and Pythagorean triples, sets of three counting numbers, a, b and c, that have the property a² + b² = c².

1. Introduce square numbers using PowerPoint 1. Animate slide 1 to build up the set of square numbers to 16. Focus students’ attention on the geometric structure:
   •  a square number of tiles form a square 
   • the symbolic notation used, for example, 5² = 5 x 5. 
2. Challenge students to create a list of the first 20 square numbers. Encourage the use of calculators to do so. You might introduce the use of the x² function using slide 2. 
3. Once students have compiled a list of square numbers, use slide 3 to check the result.       
   Introduce an example of two square numbers adding to another square number. The example given is 64 + 225 = 289 so 8² + 15² = 17². Challenge students to find other triples of square numbers. Ask them to record any examples using squares notation.
4. Allow time for students to identify some triples before using slide 4 to check answers. Introduce the term “Pythagorean triple” and ask students to spend 5 minutes researching the venerable Greek mathematician.
5. Use slides 5 and 6 to show the inverse process of finding the square root of a number. Relate square root to the side length of a square with a given area.
6. Let students attempt the problem on slide 7. They might draw the diagram using the squares in their exercise book. Alternatively use Copymaster 1.
7. Provide students with Copymaster 2. Ask them to measure and record the side length of each triangle in whole numbers of millimetres or decimal numbers of centimetres, e.g., 7.6 cm. Students should record the measures on the sides of the triangles.
8. Roam as students work. Check that they measure accurately and record the measures correctly. Ask students if they can name the types of triangles on the copymaster, such as right-angled, equilateral, scalene or obtuse-angled. 
9. Gather the class to check measurements and retain the student copymasters for Lesson 2. 

Session 2

In this session students revisit Pythagorean triples, sets of three counting numbers, a, b and c, that have the property a² + b² = c². They connect Pythagorean triples to the side lengths of right-angled triangles. 

1. Use PowerPoint 2, Slide 1 to introduce three true or false equations. Let students decide whether, or not, each equation is true. The non-example of inequality is just as important as the two examples of equality. Animating the slide gives a check of the answers.
2. Slides 2-5 use the numbers in the equalities and non-equality as the side lengths of triangles. With slide 2, pose this problem:       
   Draw a right-angled triangle that has 9 cm and 12 cm as the lengths of the two shortest sides. How long is the hypotenuse, the longest side?       
   Let students draw the triangle in their quad book, then share the length of the hypotenuse (animate the slide). Remind the students that (5, 12, 15) is a Pythagorean triple.
3. Slide 4: Discuss why (7, 10, 13) is not a Pythagorean triple (49 + 144 ≠ 169). Challenge the students to:       
   Draw a triangle that has side lengths of 7 cm, 10 cm, and 13 cm.        
   Why is drawing the triangle difficult?       
   What kind of triangle have you drawn? (Students should note that the triangle does not have a right-angle)       
   You might show students how a pair of compasses and a straight edge can be used to create the (7, 10, 13) triangle, in the ancient Greek tradition.
4. Slide 5: How do you know that (8, 15, 17) is a Pythagorean triple?       
   Draw a right-angled triangle that has 8 cm and 15 cm as the lengths of the two shortest sides. How long is the hypotenuse, the longest side?       
   Let students draw the triangle in their quad book, then share the length of the hypotenuse (animate the slide).
5. Distribute the students’ sheets of Copymaster 2. Slide 6 shows the six triangles.       
   Check your measurements.       
   Is it true? For any triangle, the squares of the two shortest sides add to the square of the hypotenuse.       
   Give an example. For triangle A, is it true that 51² + 52² = 72²?
6. Give students time to check all 6 triangles in Copymaster 2. Roam as they work. Look for:
   • Systematic recording of the results with accurate calculation (using a calculator)
   • Noticing that the claim is true only for right-angled triangles.
7. After a suitable time, gather the class to discuss if the claim is correct.        
   Can we change the claim, so it is always true?       
   “For any right-angled triangle, the squares of the two shortest sides add to the square of the hypotenuse.”
8. Look at triangles A, B and F. Does the claim still hold if we convert the measures in millimetres to centimetres?       
   For example, the side lengths of triangle A are 5.1 cm, 5.1 cm, and 7.2 cm. Is this correct? 5.1² + 5.1² = 7.2² (Yes)       
   Note that measurement is not exact so there is usually some small error.
9. You might look up a video about Pythagoras’ Theorem online to show your students. For example, this video from Math Antics is informative and engaging: https://www.youtube.com/watch?v=WqhlG3Vakw8       
   Alternatively, you can use slide 6 to discuss the special case of the (3, 4, 5) triangle. The diagram shows the geometric connection between the square numbers and the area of squares. Slide 7 shows the theorem written formally.
10. Finish the lesson with the problem on slides 8-9. Use Copymaster 3 to provide students with a scale drawing. Each sheet has four drawings.
11. After sufficient time gather the class and share answers. Slide 10 provides some solutions. The interior triangles have short sides of 2 m and 1.33 m and 2 m and 0.66 m respectively.

Session 3

In this session students revisit the geometric representation of Pythagoras’ Theorem and apply the theorem to finding unknown hypotenuses.

1. Begin with slides 1 and 2 of PowerPoint 3.       
   Slide 1: Is this triangle a right-angle triangle? How do you know?       
   Students should recognise that the yellow triangle does not look to have a right angle. That is confirmed using Pythagoras’ Theorem as 5² + 6² ≠ 7² (25 + 36 = 61 not 49).       
   Slide 2: Is this triangle a right-angle triangle? How do you know?       
   Students should recognise that the yellow triangle looks to have a right angle. That is confirmed using Pythagoras’ Theorem as 6² + 8² = 10² (36 + 64 = 100).
2. Use slide 3 to model solving an unknown hypotenuse problem, as follows:       
   A biplane is 60 metres above the ground when it is 300 metres horizontally from the take-off point.       
   What distance, d, has the biplane flown to get to where it is?       
   Ask students to record with you as the solution steps are shown (mouse click the slide).
3. Provide students with Copymaster 4 that contains a variety of problems about using Pythagoras’s Theorem to find unknown hypotenuses.       
   Roam as students work, either individually or in small teams, looking for the following:
   • Do students identify the longest side of each right triangle, irrespective of orientation?
   • Do they have a sense of the potential length of the side from the context?
   • Do they use a calculator to sum the squares of the two shortest sides and each triangle?
   • Do they use the square root function, on that sum, to find the length of the hypotenuse?
   • Are they developing a sense of the usefulness of Pythagoras’ Theorem in real-life contexts?
4. Use slides 4-11 to review students’ answers to the problems.
5. For students who need more practice use Copymaster 5.

Session 4

In this session students use Pythagoras’ Theorem to find unknown shorter sides of right triangles.

1. Record Pythagoras’ Theorem on the board and ask the class to provide an example of a right-angled triangle with correct side lengths.       
   Pythagoras’ Theorem       
   "For any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.”       
   a² + b² = c²
2. Use slide 1 of PowerPoint 4 to practice some algebra skills. The six examples require students to apply inverse operations needed to work with Pythagoras’ Theorem.
   • Set 1: Applying subtraction to both sides of the equation:  
     • a + 36 = 95       
       a = 95 - 36       
       a = 59  
     • 54 + b = 81       
       b = 81 - 54       
       b = 27
   • Set 2: Applying square root to both sides of the equation:  
     • c² = 100       
       c = 10  
     • d² = 289       
       d = 17
   • Set 3: Applying subtraction then square root to both sides of the equation:  
     • 5² - 3² = g²      
       g =$\sqrt{5^2-3^2}$     
       g =$\sqrt{25-9}$
       g =$\sqrt{16}$
       g = 4
     • 13² - 5² = h²      
       h =$\sqrt{{\mathrm{13}}^2-5^2}$     
       h =$\sqrt{169-25}$
       h =$\sqrt{16}$
       h = 12
3. Use slide 2 to introduce the yacht anchor problem.   
   The length of the anchor chain is 13.4 metres.    
   The fishing boat’s drone shows the distance of the anchor from the ship is 7.6 metres.   
   How deep is the water?   
   Ask students to draw a scale drawing of the situation, using 1 centimetre in their quad book to represent 1 metre. They will need to use the information that the chain forms a 55.5⁰ angle with the seabed. A protractor is needed to create an accurate scale drawing.   
   Use your scale drawing to estimate the depth of the water.   
   Students should get estimates of about 11 metres.
4. Work through a model of working out the depth of the water using slide 3. Ask students to record the steps as you do and justify why each step is made. Leave them to calculate the square root of 13.4² - 7.6² using their calculator, checking to see the syntax is correct. Ensure the square root function is applied to all of 13.4² – 7.6².
5. Another example of using Pythagoras’ Theorem to find a missing shorter side is provided on slide 4 of PowerPoint 4.   
   A-framed houses are ideal for mountain environments where there is a lot of snow.    
   Why are they ideal?   
   Use the measurements provided to find the missing height of the house, h.
6. Give students adequate time to attempt the problem independently, or in small teams. Slides 5 and 6 provide the solution steps that can be shared during a discussion about answers.
7. Provide students with Copymaster 6 to work on. Roam as they work, looking for the following:
   • Do they identify the given side lengths in the right-angled triangle specified?
   • Do they follow the algebraic steps as modelled?
   • Do they check for the reasonableness of their answer, in context?
8. After a suitable time, gather the class to process answers and strategies. You might use slides 7-10 to do so. Answers are:
   • Slide 7 (Marquee Tent): l = $\sqrt{{2.8}^2-{2.4}^2}$= 2.33(2dp)
   • Slide 8 (Uira Expressway): l = $\sqrt{{25.9}^2-{19.3}^2}$= 17.27(2dp). Since 19.3 + 17.27 = 36.57 the claim is correct.
   • Slide 9 – Here are some triangle lengths.   
     
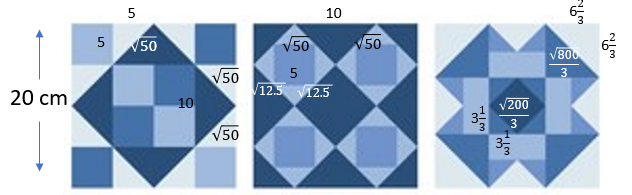
   • Slide 10 – Small Pizza d = 5.85 cm, Medium Pizza d = 8.79 cm, Large Pizza d = 10.25 cm.
9. For students who need more practice use Copymaster 7.

Session 5

In this session students use Pythagoras’ Theorem to investigate the rectangles that are possible on a 5 x 5 geoboard.

1. Use slides 1 and 2 of PowerPoint 5 to introduce the investigation. Students need to know that squares are included in the class of rectangles.
2. Provide students with Copymaster 8 which is a sheet of 5 x 5 geoboards to work on. Let students investigate the problem. Roam as they work, looking for: 
   Do they use l x w to calculate areas of rectangles? 
   Do they restrict themselves to rectangles with vertical and horizontal sides? 
   If they create ‘tilted’ rectangles do they apply fractions of squares to find total area? 
   If they create ‘tilted’ rectangles do they apply Pythagoras’ Theorem to find side lengths then total area?
3. At any point, use slides 3-5 to provoke students’ thinking and extend the investigation. After students have attempted the investigation, use slides 3-5 as prompts for reflection. Application of Pythagoras’ Theorem is a key aim of the investigation.
4. Use slides 6-8 to show how to calculate the area of a tilted rectangle. Pythagoras is used to establish the lengths of sides. Then the side lengths are multiplied to give the area. In the case of the $\sqrt{18}\sqrt{8}x$rectangle, the area is easily checked by counting squares and half squares. 
   You may decide to show students how rules of indices can be used to find the area, but that is an extension at this level.
5. Ask students to apply Pythagoras’ Theorem to find the areas of rectangles on slide 9. 
   Discuss how each side length can be found. Animating the slide provides solutions. Slide 10 provides a display of how to use Pythagoras Theorem to find one side length for the second rectangle.
6. Use slide 11 to introduce an assessment task for students to attempt individually. The problem can be attempted with different levels of sophistication. At a basic level Pythagoras’ Theorem can be applied to get a maximum length of $\sqrt{{1.2}^2+{2.4}^2}$= 2.68m. However, that length is diminished if a student considers the length that is lost due to the width of the legs. Effectively 2 cm in length is lost at each end, meaning the total length of the ladder can be no more than 2.64 cm.
7. Slides 12 -13 provide interesting spiral patterns created with right-angled triangles. Invite students to find the missing side lengths in the first spiral. Using a ruler  students might recreate the spiral in their quad books. 
   The spiral on slide 13 can also be created by students. However, invite the students to create a list of the square roots (in red) and express those roots as decimals using their calculator.  
   Which decimals terminate (finish)? (The roots of 4 and 9 are well known examples.) 
   Many of the decimals do not terminate so are irrational numbers, such as  $\sqrt{2}$,  $\sqrt{3}$,  $\sqrt{5}$,  $\sqrt{7}$
8. Slide 14 shows one of a multitude of geometric proofs of Pythagoras’ Theorem, displayed as a video. Discuss the animation, pausing at key points to ask students what they notice. The end of the video shows the equality, a² + b² = c². 
   You may wish to challenge your students recreate the proof by drawing and cutting out the two squares and four triangles involved. Alternatively view this Geogebra tool example that shows how alterations to the squares makes no difference to the efficacy of the proof.
9. Slide 15 shows the set of Pythagorean triple with side lengths up to 100. Students might used the list to draw right-angled triangles. 
   A Pythagorean Triple is a triple of natural numbers (a,b,c) such that 
   a² + b²  = c² 
   The following is a list of all Pythagorean Triples where a, b, c are all no larger than 100; 
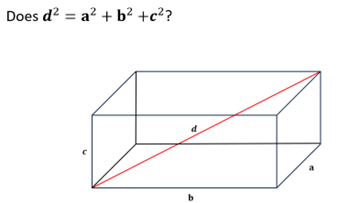
   (3,4,5), (5,12,13), (6,8,10), (7,24,25), (8,15,17), (9,12,15), (9,40,41), (10,24,26), (11,60,61), (12,16,20), (12,35,37), (13,84,85), (14,48,50), (15,20,25), (15,36,39), (16,30,34), (16,63,65), (18,24,30), (18,80,82), (20,21,29), (20,48,52), (21,28,35), (21,72,75), (24,32,40), (24,45,51), (24,70,74), (25,60,65), (27,36,45), (28,45,53), (28,96,100), (30,40,50), (30,72,78), (32,60,68), (33,44,55), (33,56,65), (35,84,91), (36,48,60), (36,77,85), (39,52,65), (39,80,89), (40,42,58), (40,75,85), (42,56,70), (45,60,75), (48,55,73), (48,64,80), (51,68,85), (54,72,90), (57,76,95), (60,63,87), (60,80,100), (65,72,97).
10. Students might also investigate if Pythagoras’ Theorem holds in three dimensions. Get a cuboid shaped cardboard box, for example a shoebox. Measure the edge lengths. Then measure the length of a piece of string that goes for one corner to the diagonally opposite corner. Slide 16 shows the problem as a diagram.