Spoilt for Choice

The questions in this activity explore multiplication as a Cartesian product (cross product), named for the famous French mathematician Rene Descartes, who invented the number plane. The Cartesian product gives the number of different combinations to be found where items from two different sets are matched one to one.
You could introduce this concept to your students by asking them to imagine someone matching 4 different tops (red, blue, yellow, and green) with 3 different pairs of shorts (red, blue, and yellow). How many different combinations could they make?
The possibilities could be modelled with cubes by organising the members of each set in a table or matrix:

The table shows that 4 x 3 = 12 different combinations are possible. Next, have the students imagine that the person acquires another pair of shorts. Ask How many combinations are now possible? (4 x 4 = 16). So in general, if n objects are matched in one-to-one correspondence with r objects, there are n x r possible combinations.
In Spoilt for Choice, the questions involve combinations of items from three sets, not two as in the example above. The combinations in this case can be shown on a tree diagram, viewed as a 3-dimensional space, or represented in a chart like the one above but with the third set of items included in each cell. Each of these three representations could be introduced using a simplified problem: one in which there are fewer choices (say 2, 2, and 2).
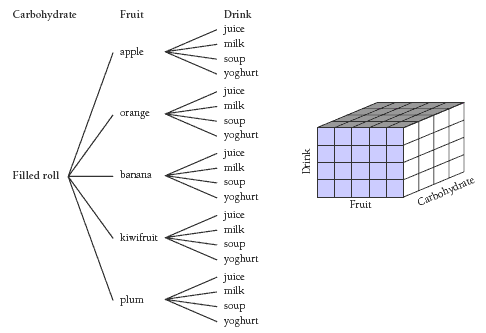
A complete tree diagram showing 4 x 5 x 4 = 80 combinations would be large but can be drawn easily using a computer drawing program and grouping, copying, and pasting repeated items. The partial tree diagram below shows the combinations of fruit and drink that could accompany a filled roll. There are 20 such combinations, and all 20 could equally well accompany any of the 4 carbohydrate options, so that is 4 x 20 = 80 combinations in all.

A cuboid can be used to represent the combinations. Each of the small cubes represents a particular combination of the three items. The number of small cubes is 4 x 5 x 4 = 80. As the cuboid shows clearly, the number of combinations for n, r, and p objects matched in one-to-one correspondence is n x r x p.
The diagram in the answers for question 1a shows how a 2-dimensional chart can be adapted to include a third set of options.
The number of combinations for the new menu is 4 x 5 x 4 = 80. 80 ÷ 5 = 16 school weeks, which is more than 1 term, so the tuck shop’s claim is true.
Question 3 requires the students to anticipate the effect of adding one more item to the menu. If the item is another fruit, then the number of different combinations will be 4 x 6 x 4, which is 4 x 1 x 4 = 16 more than previously. Adding another  carbohydrate or drink will produce 5 x 5 x 4 or 4 x 5 x 5 combinations, which is 4 x 5 x 1 = 20 more than previously. Given that there are only two possibilities (add a fruit or add a carbohydrate or drink), the students can quickly compare the effect of each.
Question 4 tests students’ understanding of the ideas developed in the earlier questions. If it is assumed that there is a choice of items in each category, there must be a minimum of 2 in each list: 2 x 3 x 3 x 3 = 54, 2 x 2 x 3 x 5 = 60, and 2 x 2 x 4 x 4 = 64 are three possible answers.
Question 5 is suitable for pair or group discussion. Allowing various combinations of fillings greatly increases the number of choices. For example, suppose there were only three options: ham, chicken, cheese. With these choices alone, the filling combinations could be: ham (by itself); cheese (by itself); chicken (by itself); ham and chicken; ham and cheese; chicken and cheese; and ham, chicken, and cheese – that’s 7 choices. If a fourth option is added, there are 15 choices.

Answers to Activity

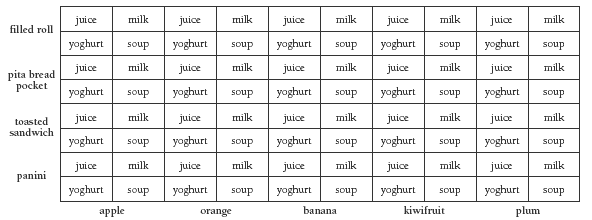
1. a. First, you’d need to add extra boxes for the extra carbohydrate and fruit items. Then, each box where the carbohydrates and the fruit intersect could be divided into 4 to include the 4 drink options. There are 4 carbohydrates and 5 fruits, so there are 4 x 5 = 20 larger boxes, or 20 combinations using carbohydrates and fruit alone. If each of those options is then subdivided into 4 for the 4 drink options, there will be 20 x 4 = 80 different options. A diagram might look like this:

b. Yes, the tuck shop’s claim is true: there are 80 different options, and a school term has no more than 55 school days in an 11 week term.
2. 4 carbohydrate options x 5 fruit options x 4 drink options = 4 x 5 x 4 = 80 combinations
3. The extra item should be a carbohydrate or a drink. Adding an extra carbohydrate or drink item would give 100 different combinations (5 carbohydrates x 5 fruits x 4 drinks = 100 combinations or 4 carbohydrates x 5 fruits x 5 drinks = 100 combinations), while adding an extra fruit would only give 96 different options
(4 carbohydrates x 6 fruits x 4 drinks = 96 combinations).
4. Answers will vary. For example, there could be 3 options for 3 of the categories and 2 for the fourth one: 3 x 3 x 3 x 2 = 54 different sandwich options. Other possibilities could include 2 x 5 x 5 x 1 = 50 or 2 x 4 x 4 x 2 = 64.
5. Discussion will vary. Allowing various combinations greatly increases the number of choices.