Simple Angles

Session 1

In this session we draw on students’ prior knowledge of rectangles, triangles, and turns. We explore 180° angles and possible turns within rectangles, types of triangles, and the concept that three angles of any triangle add up to 180°. 

1. Present students with a model or drawing of a rectangle. Discuss the size of the corner angles as being equivalent to quarter turns. Be aware of your students’ prior knowledge of the terms ‘angles’ and ‘quarter turns’. You might ask students to work with a partner to demonstrate a right angle, quarter turn, and the angles within a square (i.e. 90 °).
   What properties does a rectangle have?
   How would you describe the corners (vertices), sides and faces?
   What can you tell me about the angles of a rectangle? (quarter turn, right angle/square angle)
2. Ask students to share their knowledge of the term ‘degrees’. They might make connections with contexts like cooking and orienteering. Explain to students that degrees can be used to measure turns or angles. If a full-turn is 360 degrees then a quarter turn is 90 degrees. Present students with a model or drawing of a circle, and demonstrate what portion of the circle is one quarter. You could also ask students to stand and demonstrate a full turn, and a quarter turn.
3. Present students with a model or drawing of a rectangle. 
   Now look at the side of a rectangle. 
   If we were facing this way along the side of a rectangle, what would we have to do to be facing in the opposite direction? (Make a half turn.)
   How many degrees do you need to turn to make a half turn? (180°)
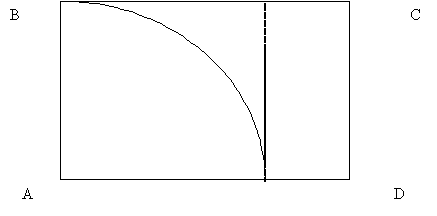
   Show me a 180°  turn on this rectangle. Students should demonstrate starting the angle on one side of the rectangle and drawing an arc to end the angle on the opposite side of the flat line - see the image below). Explain to students that this angle is ‘the spread between two rays’ or ‘an amount of turning’.
   
   Can you show me something else in this room that we could measure a 180° angle on? (e.g. whiteboard, desk - anything with a flat surface). 
   Can you show a turn through 180° clockwise and anticlockwise?
   Make sure that students can see that straight lines are 180° and that that is the same as a half turn in either direction. They should equate 180° as being the same as a half turn in a clockwise or anticlockwise direction.

If necessary, you could stop the session here. The next session would then begin with a review of 180° and the angles within a rectangle, before introducing types of triangles and angles within a triangle. 

4. If continuing on with the session, show the class the scalene triangle shown below. Label the triangle ‘scalene’ and tell the students that this means ‘no sides or angles are equal’.
    
   Talk about the angles in a triangle.
   How many angles does a triangle have? Encourage students to think about the 180° angles that were measured previously.
   How big do you think the angles are? (Bigger or smaller than 180°?) You could draw a 180° angle to scaffold students in their estimations. 
5. Tear off the angles (corners) and show that they can be put together to make a straight line or 180°.
    
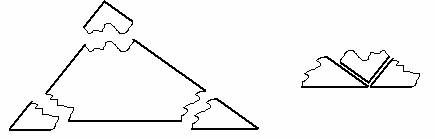
   Does this work for all triangles or was my triangle special in some way
   Do you think all three angles of every triangle add up to 180°?
6. Set the students the task of testing out that idea. Present the students with Copymaster 3. Briefly name each type of triangle. Ask students to do the following:
   1. form groups
   2. draw a number of triangles (they could choose which type to draw, or you could ask certain numbers of students to draw the different types)
   3. cut out the triangles
   4. tear off the three angles in each triangle
   5. stick them together to see if the angles make up 180°
7. When they have each examined at least three triangles, get them back together to see what results they have.  They should all have found that the three angles of any triangle add up to 180°. 
8. Display Copymaster 1. Discuss the differences between the two triangles shown. Concentrate on the fact that the angles on each triangle add up to 180°.  Then talk about the angles being less (acute angles) of more blunt (obtuse angles), especially in relation to a quarter turn (90°). You might draw a 90° corner on each corner of the triangle to demonstrate this. 
9. Put the chart on the wall.

Session 2

1. Recall the important aspects from the last lesson:
   • the angle size of a straight line is 180°
   • the sum of the sizes of the angles in a triangle is 180°
   • a triangle can have acute (less than a quarter turn) and obtuse (more than a quarter turn) angles.
2. Take a rectangle and cut it in half to make two smaller rectangles (see diagram below – cut along the dotted line).  Use paper that is slightly see-through (e.g. grease-proof paper), or draw one rectangle on paper and one on a plastic pocket. You could also display the two rectangles digitally (e.g. on PowerPoint). Put the two smaller rectangles close to each other.  Point out that you now have two angles (marked 'X' in the diagram) that add up to 180°. Get the students to draw the same diagram on whiteboards or paper.
    
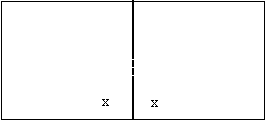
   What is the size of each of these angles in degrees? (90°)
   Why? (They are both equal and add to 180°. A half of 180 is 90.)
   Can you show me any more angles here that are equal to 90°?
3. Get the students to point to, or circle, the two original 90° angles plus the remaining six 90° angles (i.e. each corner of each rectangle).
   Why do you think that these angles are equal to 90°? (You can put the rectangles on top of one another, and the angles will be the same - demonstrate this with your rectangles)/
4. We call angles that measure 90° right angles. When we do a quarter turn, we turn 90°. A quarter turn is called a right angle.
   Can you tell me anything that you know that has right angles? (students might suggest geometric shapes and objects such as doors and windows.)
5. Organise the students into groups. Ask them to generate a list of at least 10 things, other than those discussed as a class, that have right angles. 
6. Compile a list from the students’ suggestions and put it on a chart.
7. Now we want you to think about acute angles. Remember - acute angles are smaller than right angles. You could refer to the chart from Copymaster 1 to remind students of this.
   Can someone draw me an acute angle?  (Display Copymaster 1 and a right angle for students to compare their angles to.)
   How many degrees does an acute angle have? (Answers will vary - an acute angle is less than 90°.)
   How many degrees does an obtuse angle have? (Answers will vary - An obtuse angle is greater than 90°.)
8. Take a rectangle and cut it along a diagonal, from the top left corner to bottom right corner.
   What can you tell me about the two triangles that we have produced? (They have a right angle, the other angles are acute angles.) Circle and label the different types of angles students identify. Label the triangle as ‘right angle triangle’.
9. Get the class to work in their groups to produce a variety of right-angled triangles.  Encourage them to make the triangles as varied as possible (skinny and fat, and tall and short).  Ask them to think about the following questions and have an answer ready:
   Do all your right-angled triangles have one right angle?
   Do they all have two acute angles?
   Do they have any obtuse angles? (They should not have any angles greater than 90°).
   What can you do with two right-angled triangles that are exactly the same?
   What can you say about the sum of the two angles in a right-angled triangle that are not right-angles?
10. As a class, look at the variety of right-angled triangles that have been produced.
    Then discuss what can be said about all of these triangles:
    Do they all have one right angle? (Yes
    Do they all have two acute angles? (Yes)
    Do they have any obtuse angles? Why?  (No. Encourage students to discuss their ideas with reference to their triangles. If one angle in their triangle was obtuse (i.e. greater than 90°), the sum of that angle and the right angle would be bigger than 180°. But we know that the sum of the angles of a triangle can only add up to 180°. You could ask students to draw new triangles. Ask them to modify their triangle drawings by modifying one angle to be obtuse, but keeping one right and one acute angle - they will discover that it is impossible. A triangle cannot have both obtuse and right angles, as the sum of the three angles cannot exceed 180 degrees.)
    What can you do with two right-angled triangles that are exactly the same? (Put them together to form a rectangle.) Demonstrate this, and ask students to demonstrate this with their triangles. 
    What can you say about the sum of the two angles in a right-angled triangle that are not right-angles? (Their sum is 90°/they form a right angle.) Ask the students to use the two triangles that they have put together to form a rectangle. Ask them to circle the adjacent acute angles that form a right angle. Demonstrate this with your own triangles.

Session 3

1. Remember how we showed a right angle? (We cut a 180° angle (straight line on a rectangle) in half, we put together two acute angles in triangles, we did a quarter turn.)
   What sized angle would we get if we cut a 90° angle in half? How many degrees would it have? Why? (45°, 45 is a half of 90.)
   What would it look like?
   Show me using as many ways as you can. Pair students up and ask them to demonstrate a 45° turn. Consider pairing up students with different levels of mathematical knowledge and confidence to encourage tuakana-teina. Students might demonstrate by doing one or more of the following:

• Doing a half of a quarter turn 
• Folding a right angle in half 
• Holding two pencils together and opening them out to 1/8 of a turn
• Drawing a quarter turn on a piece of paper and drawing halfway between this on a plastic sleeve 

Ask students to share their models with the class. Check that their suggestions are about the right size and that they could find the answer fairly accurately.

1. Give students a rectangular piece of paper and, in their groups, ask them to produce a 45° angle as accurately as they can.  You will almost certainly need to give them help here. 
   There is more than one way to proceed. 
   • First, they might make a right angle by cutting a 90° angle in half. If they do it this way, they will probably not quite manage to get an accurate 45°. Get them to check their accuracy by putting the two supposed 45° angles they have produced, on top of each other.  (The accuracy of this method might be improved by doing it several times.)
   • Second, they might start with one of the right angles of the rectangle and fold it in half.  If they then cut down the fold they will get a good approximation to the 45° that they want.
   • Third, they might first try to make a square.  This can be done reasonably easily but many of them will require help to do that.  Take the rectangle and fold down the shorter edge diagonally onto the longer edge. Making a cut up from B’ parallel to CD gives a square (along the dotted line).  Using this square, a 45° can be constructed by cutting from one corner to the other.  (It might be a good idea to fold the square in half first.) Cutting off the rectangle that is not overlapped gives a square.  Using this square a 45° can be constructed by cutting from one corner to the other.  (It might be a good idea to fold the square in half first.)

2. Encourage the students to try all of these methods.
   A likely wrong way that many of them might use is to just cut a diagonal from one corner of the rectangle to the other (i.e. AC).  This can be shown not to work as the two angles produced at A are not the same size. 
3. Get the class together and discuss the various ways that they have produced their 45° angles.  Compare what they have produced by putting different angles on top of the other. Ask the students what they notice about the angles they have made.

If necessary, you could stop the session here. The next session would then begin with a review of 45° angles before continuing with the introduction of 60° angles.

1. If continuing with the session, Now give students them the task of making a 60° angle using their piece of paper. Choose one method to introduce to the class, ensuring that all students can successfully make a 60° angle. Once you have introduced the concept to the whole class, use small group teaching to scaffold any students in need of further support. Provide modelling and materials for students to develop their thinking. Meanwhile, more confident students could explore different methods of making a 60° angle.
   • Method One: Use two folds along the side of a rectangle.  When the three pieces fit each other exactly a 60° angle has been formed.  This method has a self-check as the three angles that sit on top of each must be equal and 180/3 = 60.  The difficulty here is to get the folds as equal as possible. 
   • Method Two: Produce an equilateral triangle.  This is a triangle in which all angles are equal.  So each angle must be 180°/3 = 60°.  Draw a straight line AB (see the diagram) and use the length of AB as the radius of a circle by setting the compass point at A and the pencil at B.  Then draw an arc from A and an arc from B so that they meet at C.  Connect the coners ABC. ABC is an equilateral triangle and all of its angles are 60°.
      
   • Method Three: Make a regular hexagon by a compass construction.  As regular hexagons have internal angles of 120°, folding them in half gives 60°.  The construction for this is as follows:
     First construct a circle and mark any point on its circumference. Then, using the same radius, put the point of the compass on that point and mark another point on the circumference.  Repeat until six points have been marked. These six points are the vertices of a regular hexagon.
     
      
2. Get the class together and discuss the ways that they have produced their 60° angles. 
   Which do they think is the most effective/most time consuming/easiest/most difficult/quickest method?
   Which did they enjoy doing most?
   Compare the accuracy of what they have produced by putting the different angles on top of the other.
3. Summarise what has happened today.  They now know about 45° and 60° angles and how to produce them.  Use their comments to make a chart that outlines the key ideas of the lesson.

Session 4

1. Ask students to pair up and discuss what they know about angles in a triangle, and review, as a class, the angle sum of a triangle.  Emphasise that the sum of the angles of every triangle is 180°.
   What is the angle sum of a square?
   What is the angle sum of a rectangle?
2. Show the angle sum of a square and a rectangle is 360° by (i) adding four lots of 90°; and (ii) tearing off the angles of a rectangle and putting them together (repeat with a square).  Ask students to do (ii) with their partner - with one student working with a rectangle, and one student working with a square. Ask students to compare their torn-off angles with a partner. Draw attention to how the four 90° angles make two straight lines (one horizontal and one vertical when put together around one point). This can be represented as 2 x 180° = 360°.  Emphasise that the angles fit together around a 'point'. So the angle at a point is 360°.  This could be added to the wall chart.
3. Think about the fact that the angle sum of any rectangle is 360°.  Ask:
   What might this suggest about the angle sums of other four sided shapes? (That every four-sided figure has an angle sum of 360°.)
   How would we test this? (By drawing some quadrilaterals and checking to see that they add together at a point.)
4. Organise students into small groups. Let the groups draw whatever quadrilaterals (four sided, flat shapes) they like and check their angle sums. They could draw the quadrilaterals from Copymaster 4 if they cannot think of any others. 
5. Get the groups to report back on what they have found.  Do all the angles fit together round a point? Do they all add up to 360°?
6. There is actually an easy way to see that the angle sum of a quadrilateral is 360°.
    
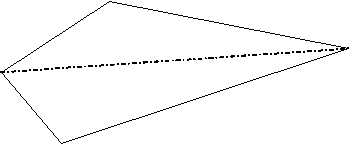
   Display the quadrilateral above and draw in a diagonal line connecting any two corners on different sides of the shape.  
   We have formed two triangles. Who can remember what the angle sum of a triangle is? That’s right, 180 °. What is the total angle sum of the quadrilateral? That’s right, it is 2 x 180° = 360°.  Help the students to replicate this on their quadrilaterals.  Ask them:
   Can you demonstrate the argument we have just used on your quadrilateral?
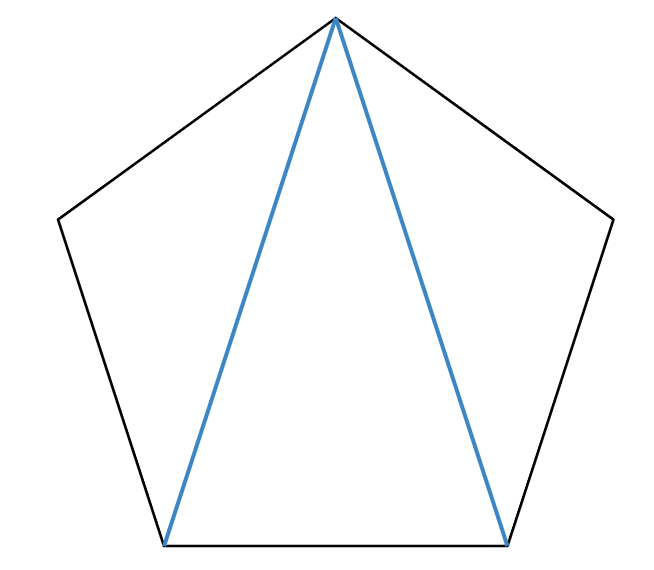
   Does it matter whether we use the diagonal above or a different diagonal?
7. What is the case for pentagons?  Remind students that a pentagon is a flat, 5-sided shape. Show them the model or drawing of a regular pentagon
   Get them to investigate the angle sum of pentagons by using any of the methods that they have used so far.  You may need to support some students in a small-group whilst others investigate this concept independently or in pairs. When they report back, look to see if they can justify their answers.  The triangle approach will work with a pentagon.  By dividing the pentagon into three triangles we see that the angle sum of any pentagon is 3 x 180° = 540° (see the image below).  The ‘tearing off of angles’ approach may be harder as it is not easy to see what 540° means.
   
8. What is the next question we should investigate?
   Get them to work on the angle sums of hexagons and report back.  This time their answer should be 4 x 180° = 720°.

9. Put the results that we have so far together in a table.  Can they see the general pattern?  What is the angle sum of any polygon?

   polygon	angle sum
   triangle	180°
   quadrilateral	360°
   pentagon	540°
   hexagon	720°

10. The angle sum of a polygon is 180° x (2 less than the number of sides).  For example - a triangle has 3 sides. Therefore, the angle sum of a triangle is 180° x 1 = 180° (because 3 - 2 = 1).  Add this to a wall chart.

Session 5

1. Recall the major things that have been done in the unit so far.  This can be done by referring to the wall charts that have been made as summaries of the various pieces of work.
2. Set them the task of making triangles with different properties, see Copymaster 2.  They will need to use the construction methods that they have used earlier to make angles of size 45° and 60°.  (Note that they can make the 45°, 45°, 90° triangle by cutting a square in half; we have already shown how to make a 60°, 60°, 60° triangle; the quadrilaterals can be made by combining these triangles in some way; the pentagons and hexagons can be made using combinations of squares rectangles and the triangles above).
3. Ask the class to report back with their findings.