Rotten Apples

In this activity, students investigate the effect of having a rotten apple in different-sized trays of apples. pples in contact with a rotten apple become rotten themselves after 1 week.
In question 1a, 11 apples are packed in the tray. The apple in the first space was rotten when it was packed. t the end of each successive week, 1 more apple is rotten. After 10 weeks, there are 1 + 10 rotten apples. After n weeks, there will be 1 + n rotten apples.
In question 1b, the position of the initial rotten apple in trays A to E has been systematically changed to encourage the students to tackle the questions in a similar systematic way.
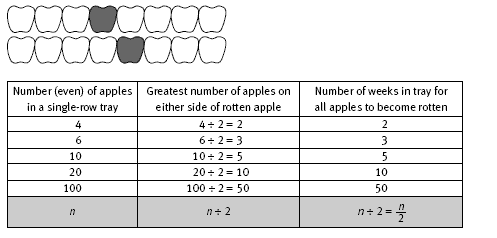
One way to approach this question is to consider the number of apples on either side of the rotten apple. For example, in tray B, we have 4 apples to the left of the rotten apple and 6 apples to the right:

In every tray, we can concentrate on the time it takes for the greater number of apples (on whichever side of the rotten apple this number occurs) to become rotten because the smaller number of apples will certainly also become rotten in this time.
So, using the results from question 1a, we can see that in tray B, it will take 6 weeks for all the apples to become rotten. A similar analysis can be used for each of the other trays.
Having considered the times taken for all of the apples to go rotten in the trays in question 1b, the students should see that the maximum time to rot will occur when the rotten apple is placed at one end of the tray. For an 11-apple tray, this will be 10 weeks (as in question 1a).
Telea then forms the rule: the maximum number of weeks it takes all the apples to become rotten is 1 fewer than the number of apples in the tray. Kathy, by letting n equal the number of apples in the tray, forms the algebraic rule: the maximum number of weeks = n – 1.
In question 1d, Kathy finds a rule for the minimum number of weeks it will take for all the apples in the tray to become rotten. She notices that this occurs when the rotten apple is packed in the middle of the tray, so there is an equal number of apples on either side of the rotten apple. When there are 11 apples, the minimum time, 5 weeks, will occur when there are 5 apples on each side of the rotten apple. The following table shows the number of weeks it takes for all apples to become rotten when there is an odd number of apples packed in a row and the rotten apple has been packed in the centre space.

When there is an odd number, n, of apples in a row, there are (n - 1)/2 apples on either side of the middle apple. One apple on each side of the middle apple becomes rotten each week, so it takes (n - 1)/2 weeks for (n - 1)/2 apples on either side of the middle apple to become rotten.
The following table shows the minimum time for an even-numbered tray of apples to become rotten. This will occur when the rotten apple is packed as close to the middle as possible. So, for example, if there are 8 apples in a tray, the minimum time for all 8 apples to become rotten will occur when the rotten apple is packed in either the fourth or the fifth position in the tray.

Once again, we are interested in the greatest number of apples on either side of the rotten apple, which is n ÷ 2 or n/2. So the minimum time that an even number (n) of apples in a row takes to become rotten is n/2 weeks.
The rules above for the maximum and minimum times that a row of apples in a tray takes to become rotten
can also be used to work out the minimum and maximum numbers of apples possible in trays where the apples all become rotten in a given number of weeks.
Suppose the apples all become rotten in n weeks. The minimum number of apples in the tray will then be n + 1, that is, 1 more than the number of weeks. This occurs when the rotten apple is packed in the first (or last) space in the row. The maximum number of apples that can become rotten in n weeks occurs when there are n apples on either side of the middle rotten apple. Then there are 2n + 1 apples altogether in the tray. For example, when all the apples become rotten after 27 weeks, the minimum number of apples possible is 27 + 1 = 28 and the maximum number of apples possible is 2 x 27 + 1 = 55.
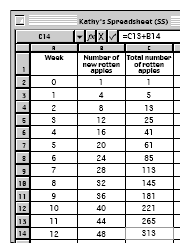
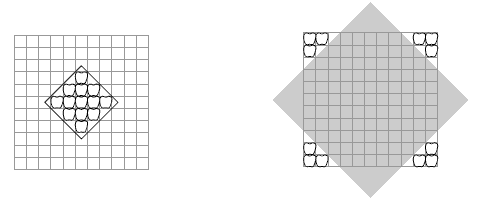
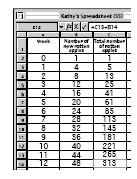
In question 2, the tray used for packing apples is more realistic. It is square-shaped with 11 x 11 = 121 spaces for apples. The students draw diagrams to show how many apples become rotten after 3 and also 4 weeks. They should notice a sequence, 4, 8, 12, 16, … , for the numbers of new rotten apples after 1, 2, 3, 4, … weeks respectively. They then use a spreadsheet to calculate the total number of apples that have become rotten after each week. They can use Kathy’s formula (4 x n) for working out the values in column B. For example, the formula in cell B3 might read =4*A3. Note that the value 1 in cell B2 does not follow this rule.

The formula =C2+B3 calculates the value for the total number of rotten apples after 1 week, =C3+B4 calculates the value for the total number of rotten apples after 2 weeks, and so on. Kathy notices that her spreadsheet indicates that 113 apples will be rotten after 7 weeks and 145 apples will be rotten after 8 weeks. So she
claims (wrongly) that all 121 apples in an 11 by 11 tray will become rotten after 8 weeks.
Kathy is incorrect because although her spreadsheet accurately counts the number of rotten apples after n weeks, it does so only for the particular diamond pattern of apples shown in question 2. Kathy’s mistake is to assume that all of the 121 apples shown in the square tray would fit within a diamond pattern of 145 apples; in fact, they would not.

Telea makes his claim of 5 weeks by using knowledge gained from the earlier work with apples in rows. He considers how many weeks it would take for the rotten apples to reach the edge of the tray and correctly calculates this to be 5 weeks. Like Kathy, however, Telea’s calculation for the time taken for all 121 apples in the tray to become rotten is incorrect because he also ignores the apples becoming rotten in the diagonals of the tray. The diagram in the Answers shows what really happens with the apples in a square-shaped tray.
Note that the corner apple becomes rotten after 10 weeks. So, as we have seen, neither Kathy nor Telea is correct.
The students might like to confirm this result by drawing a series of 11 by 11 grid diagrams that show the results after 5, 8, and 10 weeks. Having done this, they might also like to reflect on the fact that, after 10 weeks, the 121 rotten apples in the 11 by 11 tray would have grown to 221 rotten apples (as in the spreadsheet on the previous page) in a diamond pattern, had the tray been large enough to accommodate them.

Answers to Activity

1. a. 10 weeks
b. Tray A: 5 weeks
Tray B: 6 weeks
Tray C: 7 weeks
Tray D: 8 weeks
Tray E: 9 weeks
c. i. Telea’s rule could be: the maximum number of weeks it takes all the apples to become rotten is 1 fewer than the number of apples
in the tray.
ii. If a tray holds 15 apples, the longest time it takes for all the apples to become rotten is 14 weeks. So, if a tray holds any number (n) of apples, the longest time it takes for all the apples to become rotten is n – 1 weeks.
d. Kathy is correct. For an odd number of apples, placing the rotten apple in the middle will give the minimum amount of time for all the other apples to become rotten because there is the same number of apples on either side of the middle rotten apple. When a tray has n apples altogether, n – 1 is the number of apples minus
the middle apple and (n - 1)/2 stands for the number of apples on either side of the middle apple. For example, if there are 11 apples, there are (11 – 1) ÷ 2 = 5 apples on either side of the middle apple, so they all become rotten in 5
weeks. For n apples, there will be (n -1)/2 apples on either side of the middle apple, and the minimum time they will take to all become
rotten is n – 1 weeks.

e. A possible rule is n ÷ 2 or n weeks. (With an  even number of apples, for example, 20, in the tray, the minimum “rotting time” will occur when the rotten apple is as close to the middle as possible. There is no exact middle, so there are 10 apples on one side and 9 on the other side of the rotten apple. The 10 apples on one side of the rotten apple will take 10 weeks (20 ÷ 2) to become rotten. This is 1 week more than for the 9 apples on the other side.)
f. i. Minimum: 22; maximum: 43
ii. Minimum: 21; maximum: 41
iii. Minimum: 102; maximum: 203
iv. Minimum: 101; maximum: 201
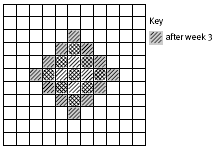
There will be 12 new rotten apples (shaded) after week 3.
2ai.

ii. 41
b. i. 4 x 7 = 28 new rotten apples
ii. The formula =C2+B3 adds the value in cell C2 to the value in cell B3 and puts the answer in cell C3 to give the total number of rotten apples after 1 week.

iii.

c. i. Kathy knows that there are 121 apples in the 11 by 11 square tray. Her spreadsheet shows that 113 apples are rotten after 7 weeks and that 145 apples are rotten after 8 weeks. So she thinks that it will take 8 weeks for the total of 121 apples in the tray to become rotten.
ii. Telea notices 5 spaces for apples on either side of the middle rotten apple. It takes 5 weeks for the apples in these spaces to all become rotten. So Telea thinks that all the apples in the tray will be rotten in 5 weeks.

iii. Both Kathy and Telea are incorrect. In the diagram below, it takes 2 weeks for the apple in the shaded square nearest the middle apple to become rotten. It takes a further 2 weeks for the apple in the next shaded space in the diagonal to become rotten. The apple in each additional shaded space in the diagonal takes a further 2 weeks than the apple in the previous shaded space in the diagonal to become rotten. There are 5 such shaded spaces in the tray, so all the apples in the tray will become rotten in 5 x 2 = 10 weeks.number of apples on either side of the middle
apple.