In this unit five-based bead strings and number lines are used to solve addition and subtraction problems. The aim is to get students that use an early additive strategy to solve problems using a tidy number strategy with 10.
- Solve addition problems like 8 + 4 = by going 8 + 2 = 10, 10 + 2 (more) = 12.
- Solve subtraction problems like 14 – 6 by going 14 – 4 = 10, 10 – 2 (more) = 8.
There are several things happening in this unit. All of them are aimed at enabling students to become more fluent when working with numbers.
The students need to realise that "making a 10" is a good strategy for solving addition problems. This strategy is reinforced by the use of bead strings and the number line, so students need to understand how these representations work, and see their relevance for addition and subtraction work.
It is important that the students gradually learn to work without the bead strings and number line, so they are encouraged to ‘image’ these objects. Instead of actually using the physical materials, they should start to think about what is happening in their heads. The next stage is for these number facts to become quickly recalled. For most students, this will take a reasonable amount of practice. In the process, students are exposed to problems in context and finally they are given examples of their own to work on.
This unit develops important mathematical thinking that is relevant to learning in school and in contexts beyond the classroom. Firstly, numbers are the base of many ideas in mathematics. It is crucial that students develop fluency in addition and subtraction, and strategies for carrying out number operations. Secondly, devices like the number line are not just useful to understand addition and subtraction, they are also used extensively in coordinate geometry where two perpendicular number lines are used as axes. In this situation they enable us to visualise quite complicated functions. Even at this early stage in school, students are developing skills that will be useful throughout their school life, as well as ideas that will grow into powerful and deep mathematics.
This unit can be differentiated by varying the scaffolding provided and altering expectations. This will make the learning opportunities accessible to a range of learners. For example:
- spending multiple lessons on each session, giving students additional time to consolidate their understandings before moving on
- having students continue to use bead strings and number lines to support their thinking, as needed
- using finger puppets to model the number line movements, and to engage your students.
Some of the activities in this unit can be adapted to appeal to students’ interests and experiences and encourage engagement. Consider adapting the addition and subtraction problems in each session to reflect current learning from other curriculum areas (e.g. trips to the marae, swimming lessons, learning about animals). Characters from shared texts can also offer engaging contexts to frame problems in. Other contexts for number line problems include:
- lines of students for kapa haka groups, with students arriving or leaving
- planting seedlings in lines, with extra seedlings to be added
- native birds sitting on a branch, with birds arriving or leaving
- trays of food being laid out for a hangi with plates being taken away as people collect a tray, and more trays being added as people prepare the food.
Numbers in te reo Māori could be introduced in this unit and used throughout other mathematical learning.
- Number line 1 - 20 (Copymaster 1)
- Bead string 1 - 20 (Copymaster 2)
- Number line 1 - 100 (Copymaster 3)
- Bead string 1 - 100
- Pegs
- Problem cards (Copymaster 4)
Note the following useful prior knowledge:
- Students have had experience making two types of facts with materials: combinations to 10 (e.g. 6 + 4 = 10, 3 + 7 = 10) and facts with a 10 (e.g. 10 + 6 = 16, 10 + 8 =18).
- Students can recall these two types of facts.
Session 1
- Begin the session by reminding the class what a number line is. Show an example of what a number line is, and encourage students to share where they have seen them before/what they have used them for. The picture books Ten on a Twig by Lo Cole and Hello Numbers! What Can You Do? By Edmund Harriss and Houston Hughes could be used to engage your students in number thinking. Pose the following problem using either English or Māori numbers.
Kahu the kiwi starts on number eight and walks along four more spaces. Where does she end up? or
Kahu the kiwi starts on number waru and walks along whā more spaces. Where does she end up? - Ask a student to come forward and place a peg on the number line where Kahu started.
How can we find out where Kahu will end up without counting?
How many spaces will Kahu need to go to get to number 10?
Now how many spaces has she got left to go?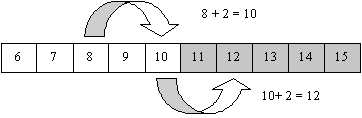
- Ask similar types of problems such as;
Kahu the kiwi is on number 9 and walks another 4 places, where will she end up?
Kiri the kea is on number 13 and flies backwards 5 spaces. Where does he end up?
Have the students predict where they think they will end up before getting students to come out and share their strategies on the number line. - Now increase the size of the starting number. For example:
Kahu has been walking for some time now. She is on number 27 and walks another 5 spaces. Where do you think she will end up?
Ask students to talk to their partner and discuss how they would work the problem out.
Challenge students to see if they can solve the problem without counting on:
See if you can solve the problem another way?
What is the nice friendly number that Kahu is going to pass through?
How far is it from 27 to 30?
Now how much further does she have to go? - Pose a few more problems that start with a larger number. Continue to model on the number line with pegs. Possible problems are:
Kiri the kea starts on 49 and slides another 8 spaces. Where does he end up?
Tāne the takahe starts at number 87 and wanders on another 8. What number does he end up on? - Send those students who have got the idea off with Copymaster 1. Give students the option of remaining on the mat with you to go over some more problems.
Session 2 – Marble Collections
Over the next three days the aim is to slowly remove the number lines and bead strings and encourage students to visualise what would happen on the bead string or bead frame. This is called imaging.
Begin by using a bead string 1-20 coloured in 5’s like this.
![]()
- Warm up. Build up students’ knowledge of the bead string so that they know such things as bead 6 is after the first set of yellow beads. We want students to be able to find these beads without counting each single bead.
Where is number 8?
Find number 11.
Where would number 16 be? - Encourage students to explain how they found where each bead was by using groupings, that is by using non-counting strategies. E.g. I knew that 11 was after 10.
- Now pose some story problems.
Moana has a marble collection. It starts with 9 marbles. Show me where 9 is on the bead string.
Moana is on a winning streak and wins 6 more marbles. How many does she have in her collection now?
Use the bead string to demonstrate putting one marble onto the 9 to make it 10 like this: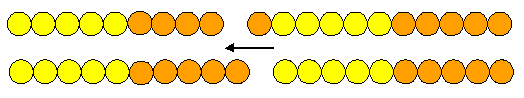
- Record together on the board:
9 + 1 = 10; there were 5 left; 10 + 5 = 15. - Continue to pose similar problems:
Kauri has 8 marbles and she wins 6 more. How many does she have now?
George has 15 marbles and wins 6 more. How many does he have now?
Hemi has 15 marbles and loses 6. How many does he have left? - Give students Copymaster 2. Show them a couple of examples of how you would show your working. Students complete the activity in pairs.
Session 3 – Do and Hide Number line
This session is to use the number line (Copymaster 3) and bead string to solve problems and then the number lines and bead strings are taken away to encourage students to start imaging.
- Talia the Tūi starts on 9 and flies forward 7 more spaces. Where does she end up?
Ask a couple of students to take the number line and pegs away and work out the answer. Ask the students remaining to visualise what the others will be doing on the number line. The following questions may prompt the students to image the number line.
Where did the Tūi start?
How far does the Tūi have to fly to get to 10? - Ask the students who took the number line away to share what they did to solve the problem.
- Repeat with other problems. The following characters could be used to create similar story problems: Kākāriki the kererū, Giana the giant wētā or Tama the tuatara.
Encourage the students to visualise what they would do on either the number line or bead string. Extend some of the problems to numbers beyond 20. - The following types of problems will continue to challenge the students further.
Start Unknown | Giana the giant wētā jumps 4 more spaces and ends up on 10. What number did she start on? |
Change unknown | Tama the tuatara starts on 3 and crawls along the number line and ends up on 8. How many spaces did he go? |
Session 4 – Problem Solving Bus Stops
In this session, problems are placed on the top of a large sheet of paper. Students move around each bus stop solving the problem. They record their working on each sheet.
- Warm up with some whole class problems like the ones that have been shared in the previous sessions. Get students to talk to their neighbour and share how they worked out the answer. Record the different ways students solved the problem by writing it on the board.
- Place each of the problems from Copymaster 4 on to a large piece of paper. Place the sheets around the room. Students can either rotate around the bus stops in pairs randomly or in a sequence to solve each problem. They are to show their thinking on the large sheet of paper.
Session 5 – Reflection
Use this session to share the solutions students came up with for each of the bus stop problems. Encourage students to act out the problems where appropriate and to remodel their answers on the number lines or bead strings.
Dear family and whānau,
This week we have been using a number line to do some addition and subtraction. Here is an example of a number line:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Ask your child to show you how they would solve this problem:
Kiri has 5 lollies. If she buys 8 more, how many does she have altogether?
Perhaps you can make up some more problems like that and work them out together. When your child gets really quick at coming up with an answer, put the number line away and ask them to try to figure out the problems by visualising the number line in their head.