Make the Highest Total
theoretically and experimentally examine the probabilities of games of chance
devise and use problem solving strategies to explore situations mathematically (be systematic, use a table).
This is a fairly straightforward problem based on an understanding of the chances involved. The problem needs to be set up in the right way but this shouldn’t be too difficult with a little help from the teacher.
The problem can be solved either empirically or theoretically. The former case means that the students need to do some experimenting or simulating. The latter case involves the hardest thing of all – thinking.
Problem
Luana is playing a game. She has 6 cards numbered 1 to 6. She has to place them into the three positions of this grid to make the highest possible total she can.
The right-most position represents the units’ column for the number that she will finally produce. The middle position is the tens’ column and the left-most position is for the hundreds.
She has to position the cards after rolling a dice. She rolled a 3 first and decided to place card 3 into the tens’ column.
She then rolled a 5. Where should she place the 5 to get the highest 3-digit number on average? [She only has 1 of each card, if she rolls another 3, or another 5, she just rolls again.]
Teaching sequence
- Play a few games informally where students play in pairs against each other.
- Pose the problem situation to the whole class.
Where is the best place to position the 5?
.gif)
- The students should observe that there are only two options, either the 5 goes in the ones’ column, or it goes in the hundreds column.
- Take as class vote for each of the options.
- Discuss with the class ways to solve the problem. List ideas on the board.
- Let the students investigate the problem in pairs or small groups.
- As the students work ask questions about their reasoning. If they are using an experimental approach ask them to think about the theoretical situation.
Could you think about this problem without playing the game?
What do you know about the chance of each number being rolled? - Ask the students to record their solution to share with others.
- Share solutions.
Extension
1. Set up a similar situation with the same game.
For example
.gif)
- What if a 3 is rolled for the second roll? Where should it be placed?
- What if all 10 digits are available i.e. 10 cards, numbered 0 to 9
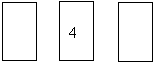
The second roll is a 5 - where should it be placed?
Solution
Method 1. Empirical. Make a table.
Try the experiment 10 times each way and record the results.
|
Left |
Right |
|
536 531 532 532 534 531 etc |
135 635 235 235 etc |
How many times does the left side of the table win over the right side?
Method 2. Theoretical
(i)
There are 4 possibilities for the next roll (635, 435, 235, 135). All are equally likely.
(ii)
The 4 possible results are 536, 534, 532, or 531.
If a 6 is thrown, 635 beats 536. However, if any other number is thrown, it is better to have the 5 in the hundreds’ column. ‘Any other number’ is thrown three times (1, 2, or 4). So on average, we would expect that the 5 in the hundreds’ column would win 3 times out of 4 (or with a probability of ¾).
Solution to the extension:
Again try it in both places to see what will happen. If you try 3 – 1 first, then you get the possibilities 361, 351, 341 and 321. If you then try – 3 1, you’ll get 631, 531, 431 and 231. Having the 3 in the tens’ column wins 3 times out of 4 on average.
With the game that uses all ten digits, we’ll assume that if 0 goes in the hundreds’ column, then it makes the number a 2-digit number. So, if we start out with 5 4 - , we can get 549, 548, 547, 546, 543, 542, 541, 540. On the other hand if we start with – 4 5, then we get 945, 845, 745, 645, 345, 245, 145, or 045. For 9, 8, 7 and 6 it is better to have the 5 in the units’ column but for 3, 2, 1 and 0 it is better to have the 5 in the hundreds’ column. In this case things come out equal.
From here you could explore the game from scratch. That is, no matter what numbers come up and in what order where is the best place to put them?
Another variation of this game is to look for the total of 10 numbers produced by rolling a dice. Does this variation need an alternative method of analysis?
| Attachment | Size |
|---|---|
| MaketheHighestTotal.pdf | 66.57 KB |
| MaketheHighestTotalMaori.pdf | 58.53 KB |
Similar Resources
Coin Shake-Up
Predict the likelihood of an event based on data collected
Use a systematic approach to find all possible outcomes
Effectively plan mathematical exploration
Grabbing CDs
Systematically count outcomes
Compare the likelihood of events
Devise and use problem solving strategies to explore situations mathematically (systematic list, draw a picture, use equipment).
Lara's Equiprobable Dice I
Find certain probabilities relating to rolling two dice
Devise and use problem solving strategies to explore situations mathematically (be systematic)
Another Dartboard
Predict probabilities of an event involving area
Make deductions from probabilities
Devise and use problem solving strategies to explore situations mathematically (guess and check, be systematic, look for patterns, draw a diagram, make a table, think, use algebra).
Dressing In The Dark
Work systematically to identify all the possible outcomes.
Describe events using everyday language.
