This is a level 4 number activity from the Figure It Out series. It relates to Stage 7 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (332 KB)
simplify a fraction
convert a fracion to a percentage
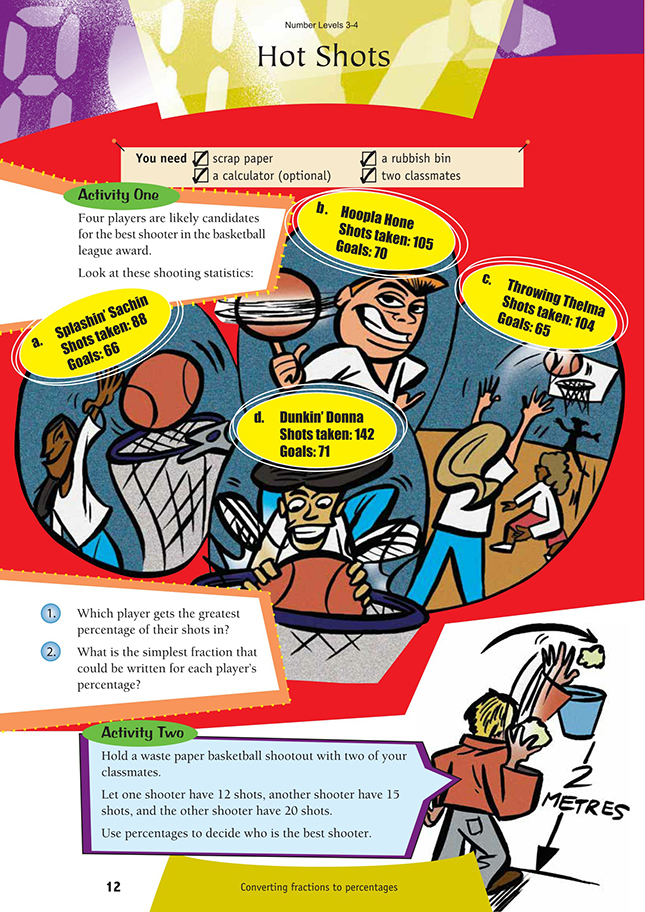
Scrap paper
A rubbish bin
FIO, Level 3-4, Number, Book 1, Hot Shots, page 12
A calculator
Two classmates
Activity One
To convert the shooting statistics into percentages, most students will probably write the statistics as a fraction and convert that to a percentage, for example, 66/88 x 100 = 75%. They may also use other strategies. For example, they may recognise that Dunkin’ Donna’s 71 goals out of 142 shots is 1/2 and know that this is 50%.
To simplify a fraction, the students need to find a number that can divide both the numerator and the denominator (with no remainder) and repeat this until there is no number that divides both these numbers. For example, with 66/88, dividing the numerator and denominator by 2 gives 33/44.
Dividing this numerator and denominator by 11 gives 3/4.
Activity Two
The students will calculate the percentages in a similar way to that in Activity One.
As an extension, the students could take turns shooting 12, 15, and 20 shots. Is there any relationship between the number of shots and the best shooter? The students could suggest reasons for this, for example:
• Players improve with practice.
• Players who have more shots get tired and so are less accurate.
• One player is more accurate than the others, no matter how many shots they have.
Answers to Activities
Activity One
1. Splashin’ Sachin (75%)
2. a. 3/4
b. 2/3
c. 5/8
d. 1/2
Activity Two
Practical activity