This is a level 4 geometry strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (247 KB)
explore fractals
- A4 paper
- scissors
- ruler
- compass
- FIO, Level 4+, Geometry, Book Two, Golden Spirals, page 23
- computer (optional)
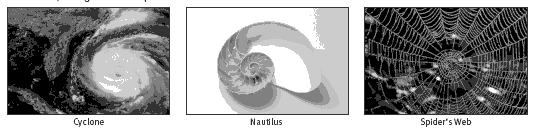
Spirals appear in surprising places and range from the very small to the huge. The cochlea (chamber of the inner ear) is a spiral. So is the nautilus shell (and the shell of many other sea creatures), the shell of a snail, the webs of some spiders, the pattern of leaf distribution around the stems of some plants, whirlpools, tornadoes, and galaxies in space.
Activity
To do the construction in question 1, the students will need a sharp pencil, a good compass and ruler, and a set square (or other suitable right-angled object). Most students should find the diagrams self-explanatory, but they will need to take great care with their construction work. Even with care, they are unlikely to be able
to complete more than 5 or 6 quarter arcs. The cumulative effect of small inaccuracies will mean that the sides of the ever-smaller rectangles are no longer in the correct ratio (j).
As an alternative to pencil and paper, the students could use a computer drawing program. Starting with a large 90 degree arc, they can construct a continuous spiral by repeating this sequence:
- copy the previous arc
- rotate the new arc 90 degrees clockwise
- enlarge (scale) it by a factor of 1/j (to reduce its size by the correct amount)
- translate it so that it joins up with the previous arc.
Students should see that each successive section of the spiral is a smaller version of the previous one. The spiral is therefore a fractal. See the final activity in this book for more on fractals.
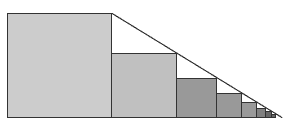
In question 2, the students investigate the squares that contain the 90 degree arcs of the spiral, not the arcs themselves. They will find that if they line them up as instructed, they can make a "ramp" down them, using a "plank" that rests on their top right-hand corners. In other words, the top right vertices of the squares are
all in a straight line. The students may like to consider how many squares they could cut (or draw) before they become too small to be visible. Surprisingly few!
Investigation
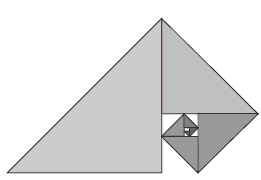
Students could make this fractal:
They start with a golden rectangle and fold down successive corners. Before making the fourth (and subsequent) folds, they will need to make a straight cut.
Answers to Activity
1. Practical activity
2. Practical activity. When lined up together, the squares will look like the following diagram. If you use a ruler, you will find that their top right-hand corners lie on a straight line.
Investigation
Practical activity