Digit Chains

This activity focuses on digit rules to form digit chains. In each chain, a rule is used to change one number into another.
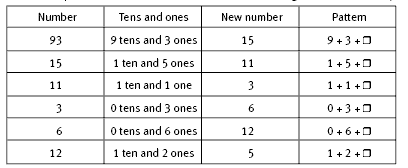
In question 1, a table like the one below may help the students to identify the digit rule. They should focus on the number of tens and ones to see if they can find a link between these values and the new number in each case. (If they follow the hint and look at the rules for questions 2 and 3, they will see that an operation such as addition or multiplication is carried out on one or more of the digits in each number.)

The values that go in the empty boxes in the table are the values for the number of ones. So the new number 15 is found from 9 + 3 + 3, the new number 11 is found from 1 + 5 + 5, and so on. The digit rule is: double the ones digit and add the tens digit.
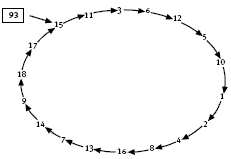
The starting number, 93, becomes 15 where it enters the loop. A diagram of the loop is shown in the Answers.
Notice that the loop includes all the numbers from 1 to 18. The number 19 is not in the loop. It stays as 19 when the digit rule is applied: 19 →1 + 2 x 9 = 19
The next number, 20, enters the loop at 2, the number 21 enters at 4, the number 22 enters at 6, and so on. Multiples of 19, however, all eventually produce 19 when the digit rule is applied. For example, 95 = 19 x 5, so it is a multiple of 19. Applying the digit rule gives the following: 95 → 9 + 2 x 5 = 19
The number 399 is also a multiple of 19 because 399 = 19 x 21. The digit rule is applied to tens and ones, so we think of 399 as 39 tens and 9 ones rather than as 3 hundreds, 9 tens, and 9 ones. The digit rule then produces the following: 399 → 39 + 2 x 9 = 57 → 5 + 2 x 7 = 19
So multiples of 19 do not enter the loop.
In question 2b, the students will find that 2-digit numbers reduce to a single-digit number from 1 to 9.
For example, three successive applications of the digit rule reduce 67 to 4. Note that there is no change when the digit rule is applied to the single digit 4.

67 →6 x 3 + 7 = 25 →2 x 3 + 5 = 11 →1 x 3 + 1 = 4 →0 x 3 + 4 = 4

The first 3-digit number is 100, which is 10 tens and 0 ones. So 100 becomes 10 x 3 + 0 = 30. This reduces to 3 x 3 + 0 = 9. The 3-digit number 263 = 26 tens and 3 ones. So 263 becomes 26 x 3 + 3 = 81. This reduces to 8 x 3 + 1 = 25, which reduces to 2 x 3 + 5 = 11, which in turn reduces to 1 x 3 + 1 = 4 (as per the example for 67 above). 3-digit numbers all reduce to 2-digit numbers when the rule is applied, so they also reduce to single-digit numbers from 1 to 9.
4-digit numbers also change in the same way. For example, 2 317 = 231 tens and 7 ones. So 2 317 becomes 231 x 3 + 7 = 700. This number reduces to 70 x 3 + 0 = 210, which then reduces to 21 x 3 + 0 = 63. Further use of the rule gives 6 x 3 + 3 = 21, which reduces to 2 x 3 + 1 = 7. So, just as with 3-digit numbers, all 4-, 5-, and 6-digit numbers and so on reduce to a single-digit number from 1 to 9.
In question 3, the loop is never ending, so any number that enters the loop can be changed into any number in the loop. For example, 43 changes to 35, which changes to 40, then 20, then 10, then 5, then 25, and then 35, where it first entered the loop. Zara concluded that since all four of her chosen starting numbers entered the loop, then all numbers enter the loop. In fact, she is not correct. Multiples of 3 (that is, 3, 6, 9, 12, …) don’t enter the loop. Those that are also multiples of 9 (that is, 9, 18, 27, 36, …) become 45, which itself becomes 45 because this is a loop with only one value, and the others enter a loop that includes only 30 and 15. Notice how 30 changes to 15, which then changes back to 30:
30 →3 x 5 + 0 x 5 = 15 → 1 x 5 + 5 x 5 = 30

Answers to activity

1. a. The digit rule is: double the ones digit and add the tens digit to it. The numbers after 5 in Mika’s chain are: 10, 1, 2, 4, 8, 16, 13, 7, 14, 9, 18, 17, 15, 11, 3, 6, and 12. These numbers form a loop.

b. Up to 190, the multiples of 19 reduce to 19. After that, they reduce to a multiple of 19 and eventually reduce to 19 itself. For example,
133 → 19 and 209 → 38 → 19.
2. a. Answers will vary. For example, for 43, the chain becomes: 43, 15, 8, 8, …
b. 2-digit numbers reduce to single-digit numbers from 1 to 9.
c. 3-digit numbers reduce to 2-digit numbers that reduce to single-digit numbers from 1 to 9.
4-digit numbers also eventually reduce to single-digit numbers from 1 to 9.
3. a. The starters that Zara has used reduce to numbers in the loop. For example, 83 becomes 25, which is in the loop. 25 becomes 2 x 5 + 5 x 5 = 35, then 3 x 5 + 5 x 5 = 40, then 20, then 10, and then finally 5.
b. Zara concludes that all numbers enter the loop. However, numbers that are multiples of 3, that is, 3, 6, 9, 12, …, don’t enter the loop. Multiples
of 3 that are also multiples of 9, that is, 9, 18, 27, 36, … , all become 45, which itself becomes 45. The other multiples of 3 enter a loop that has just two numbers, 30 and 15.
4. Answers will vary.