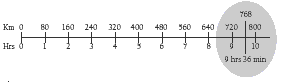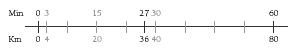Deb the Driver

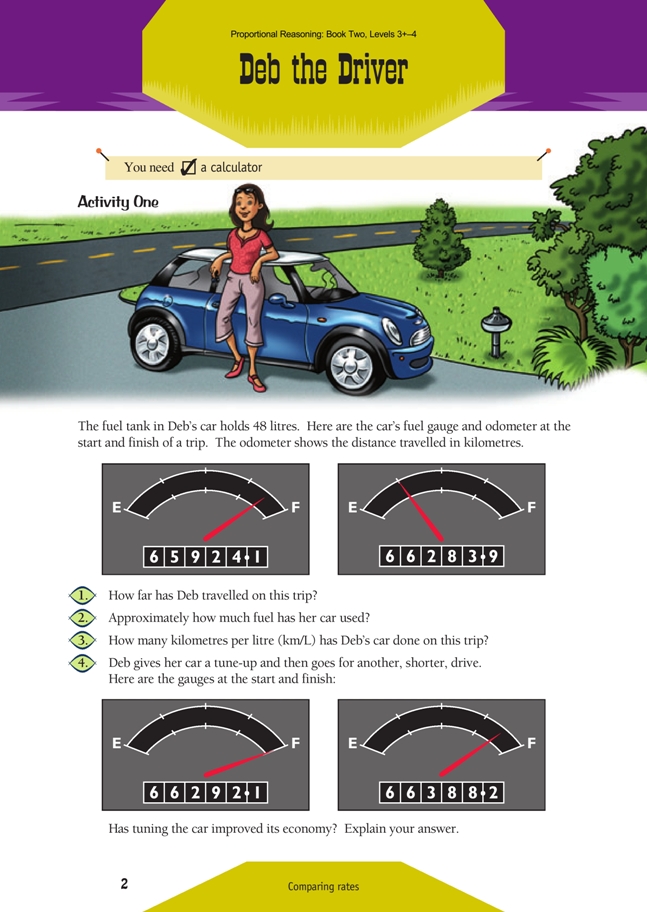
Activity One

In this activity, students calculate and compare rates in a motoring context. The numbers have been chosen so that the calculations themselves are fairly straightforward; the challenge is to work out how the different bits of information relate to each other mathematically.
Give your students the opportunity to read the introduction and try to make sense of it for themselves. Possible areas of difficulty are interpreting the scale on the fuel gauge and recognising the place value of the numerals shown on the odometer: it is easy to miss the decimal point.
When they do questions 1 and 4, encourage the students to estimate the difference in distances before using a calculator. Discuss strategies that might be used. Here is one: “The reading at the start is about 75 km less than 66 000. The reading at the finish is about 285 km greater than 66 000. 75 + 285 = 60 + 300 = 360 km. So Deb drove about 360 km.”
Encourage the students to think of different ways of making a good estimate (one that can be done in the head but that gives a clear feeling for what the answer looks like). You could restate the students’ methods and help them record them in ways that can be followed. Make a clear distinction between estimates, which point to the answer, and the answer itself.
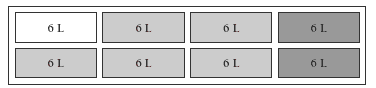
In question 2, the students need to work out the difference between the two readings of the fuel gauge. If necessary, they can do this using materials – by folding a piece of paper in half, doing this again, and then folding it a third time. They then unfold the paper to see the eighths and shade the difference between 7/8 and 1/4 to reveal the answer of 5/8.
Students could draw this model of a fuel tank, distribute the 48 L of petrol in 8 equal amounts, and then use the model to calculate the fuel used:

The shading shows that 5 x 6 = 30 L of fuel were used, so 5/8 of 48 is 30 L.
The students should also look at how the problem could be solved using number properties. If they are able to understand that 5/8 is 5 x 1/8, they can find of 48 and then multiply that amount by 5. Alternatively, they could multiply the amount of fuel by 5 (5 x 48 = 5 x 50 – 5 x 2 = 240) and then divide the result by 8. Encourage your students to try both approaches; if they understand both, they will have greater flexibility when it comes to solving other problems involving fractions.
Question 3 introduces the direct relationship that exists between kilometres travelled and litres of fuel used. Check that all your students understand the meaning of “per” and know that it corresponds to the division operation. Note that the question uses km/L as the unit because most students will find this easiest, both mathematically and conceptually. The official unit for measuring fuel consumption is litres per 100 km. Some students may be aware of this. If so, you could challenge them to work out Deb’s fuel consumption using this unit: 30 L per 360 km = 30 L per (100 x 3.6)
km = (30 ÷ 3.6) L per 100 km = 8.3 L per 100 km.
Students should attempt question 4 independently, applying the ideas discussed previously.

Activity Two

Make sure that the students have the correct answer to the previous question before they begin work on question 1a. Using it, they should form and solve the equation 16 x 48 =. They shouldn’t need a calculator to do this multiplication; the numbers lend themselves to doubling and halving or partitioning strategies.
Question 1b needs the correct answer from question 1a. Encourage your students to take the problem step by step, thinking about the distance Deb will cover in 1 hr, 2 hrs, and so on. If they do this, they will discover that she should be able to drive between 9 and 10 hrs. They will need to use their proportional reasoning skills to work out exactly when the fuel will run out. They could use a double number line as in the Answers, or an equation.
A double number line could be used to solve question 2, but the numbers are not very convenient. A simpler approach is to use ratio. 90 km are covered in 1 hr, so the distance:time (min) ratio is 90:60 = 30:20 = 3:2. This means that the car should travel 3 km every 2 min, so Deb’s car should travel 12 x 3 km in 12 x 2 = 24 min.
Question 3 tells us that Deb’s journey actually took 27 min, so her car must have been going slower than 90 km/h. Have the students study the double number line shown and match the information in the diagram with the data from the question. Ask them “What size are the steps on  the number line?” and “Why does the number line stop at 40 kilometres in 30 minutes?” (There’s no need to take the line any further because 40 km in 30 min is the same rate as 80 km in 60 min.) An alternative
approach is to use ratio, as suggested for question 2. The distance:time ratio is 36:27, which is 4:3. This means that the car travels 4 km in 3 min, which is the same as 4 x 20 = 80 km in 3 x 20 = 60 min. In other words, the car was doing a speed of 80 km/h.

Answers to Activity

Activity One
1. 359.8 km
2. About 5/8 of 48 L, which is 30 L
3. Deb’s car travelled about 360 km on about 30 L, which is 12 km/L.
4. The car has done 96.1 km on about of 48 L. That is about 96 km, using approximately 6 L. This is 16 km/L, so yes, Deb’s fuel consumption has improved.
Activity Two
1. a. The tank holds 48 L and the car now travels 16 km for each litre of fuel, so Deb should be able to drive 48 x 16 = 768 km on a tankful.
b. In 1 hr, Deb travels 80 km. So she can drive for 768 ÷ 80 = 9 3/5 hrs (9 hrs and 36 min). This can be shown on a number line:

2. 90 km/h means that the car travels 90 km in 60 min, which is 1 km each min. To cover 36 km should take 24 min. (24 x 11/2 = 36)
3. If Deb covers 36 km in 27 min, she covers 4 km every 3 min (as on the number line shown), or 8 km every 6 min, or 80 km every 60 min. This is a speed of 80 km/h.