The Cost of Credit

Financial understanding
In this activity, the students explore the use of credit cards as a way of borrowing money and the cost to a borrower of using someone else’s money. This extra money paid to the lender is called interest. This activity will help students to understand that every financial decision we make has consequences, and those consequences can be positive or negative.
Understanding borrowing through credit cards engages students in thinking about being fair and responsible because their actions impact not only on themselves but also on others. Being fair and responsible is about taking responsibility for decisions made.
In the activity, students explore what it would cost to borrow $5,000 on a high-interest credit card and how long it might take to pay that amount off (providing that none of the money paid off is reborrowed). The activity highlights the need to look carefully at the cost of various choices so that an informed decision can be made.
Although the credit card deal looks attractive in this scenario, it would take 56 months or 4 years and 8 months to pay off the $5,000, by which time the family would have paid a total of $8,322.08 to the credit card company, with $3,322.08 of that being interest payments. This information comes as quite a shock to students when they work it out! Ask them to work out how old they would be by the time the Murphys paid off their 9-day holiday.
Many students will find the concepts and calculations in this activity difficult and will benefit from working co-operatively through the questions as part of a teaching group. There are many opportunities for teacher input and discussion as they go through each question.
Mathematics and statistics / Financial understanding
Before you look at the activity together, it is worth introducing the concept of interest and compound interest to the students. The following information may be of help.
Interest can be looked at in two ways: the amount that you pay to be allowed to use someone else’s money or the amount that you earn by lending someone else (like the bank) your money.
You could introduce the idea of interest by saying: Let’s imagine that (student’s name, for example, Jim) lends me $100, which I have to repay at the end of the year. At the end of the year, I give him back the $100. Is that fair? Expect a variety of responses, for example: yes, because that’s what you owed him and you’ve paid it back, or no, because Jim didn’t have the use of the money for the year, so you should pay him some extra money because he has allowed you to use his money.
How might Jim feel about me having his money for most of the year and then giving him back the same amount? Expect a variety of responses, for example: He might feel OK about that, or he might wish he had some compensation for not being able to use his money himself for that time.
What does Jim miss out on by not having the use of his $100 for the rest of the year? He can’t spend it if he wants to; he can’t use it to invest and earn interest from someone else.
What does Jim get out of the deal? Perhaps he feels good about having helped you out by lending you the money, but he doesn’t get any financial gain. He might worry about whether he’ll get his $100 back at all.
What about if I paid him some extra money to make it worth his while financially? How much extra money do you think I should pay him? Take a class survey by getting the class to put their hands up or write the amount down when
they agree with it. Who thinks $1 extra would be fair? $5? $10? $20? $50? $75? $100? More?
You can demonstrate visually how interest is added on to the amount of the loan (the principal) by giving each student a strip of paper about 10 centimetres long. (You should probably tell them that the interest rate you are using is higher than usual, to make the mathematics easier, and that usually the borrower would be paying back
some of the principal each year.)

This strip of paper represents the amount of your loan.

You are charged 25 percent interest on your loan at the end of 1 year. Fold your strip of paper to find out how long 25 percent or one-quarter of your loan is.
Get another piece of paper, cut an amount that is the same as 25 percent of your loan, and tape it alongside. This whole strip is how much you owe the bank now after the first year.

You can demonstrate the effect of compound interest by continuing the same process:
Now another year goes past, and the bank charges you another 25 percent interest on the whole amount that you owe them. Find out how long 25 percent or 1 quarter of your amount owing is now. Cut a piece of paper to show the second year’s interest, and tape that on.

Why is the interest in the second year more than the interest in the first year? (Because it’s one-quarter of the loan  plus the previous year’s interest, not just one-quarter of the loan amount. This is called compound interest.) What would happen to the amount you owe after 3 more years if you didn’t repay any of the money? (It would get bigger and bigger!) Some students may be interested to continue to show this visually with their strips of paper. They could explore the fact that if you lend money, the converse applies.
Introduce the scenario on the page: How long do you guess it might take the Murphy family to pay back their loan? Record the guesses so that you can refer back to them later during a reflective discussion.
For questions 1d and e, one way to bring the scenario to life would be to “act it out”. Give one student a sign with InstantBuys Credit on it and $5,000 of tens money. Another student represents the Murphy family. Give a running commentary for the students to act out: Here’s the InstantBuys credit card company saying “Yoohoo! Come and borrow $5,000!” So the Murphy family say, “That’s handy”, and they borrow $5,000 (credit-company student gives them the $5,000) and go flying off to Australia on holiday (Murphy-family student flies around room). They have a wonderful time, doing lots of exciting activities. Now they’re back from holiday, it’s the end of the month, and the credit card company says, “Hey, you have to start repaying your loan now. We’ll just work out how much you still owe us … hmm … you borrowed $5,000, and we’re charging you 24 percent interest per annum, calculated monthly, that’s 2 percent a month …”
How much money do the Murphys owe InstantBuys right now? Write on the board: 2% of $5,000 =. Get the students to solve this problem in small thinking groups of 3–4, and then get them to share their solutions and strategies for solving it with the whole group. Make calculators available if needed.
Expect responses such as:
Using a known fact and building from there: “I know that 2 percent of $100 is $2, so 2 percent of $1,000 must be $20, and 2 percent of 5 000 must be 5 times that. 5 x $20 is $100.”
Finding 1 percent and doubling it to get 2 percent: “I know that 1 percent of $5,000 is $50 because one-hundredth of 5 000 is 50. I have to double that to get 2 percent of $5,000: 2 x $50 = $100.”
Using a calculator and multiplying by 0.02, which is equivalent to 2 percent: “0.02 x 5 000 = 100.”
Continue the scenario:
Now the Murphys say, “But we only have to repay $150 a month, so here it is.” InstantBuys credit says, “Thank you very much for that; we’ll send you a statement saying how much you still owe us and how much of that $150 you just paid us
was interest and how much was principal (the original $5,000 loan).”
Get the students to return to their thinking groups to work out the InstantBuys credit card monthly statement (draw a blank table on the board). Then get them to share their solutions and strategies for solving it with the whole group. Students at stage 7 should be able to do this using strategies in mental or written form, but others may need the support of tens materials or calculators.

Expect responses such as:
Amount borrowed (principal): $5,000
Amount owed after 1 month: $5,100 ($5,000 principal + $100 interest = $5,100)
Amount repaid: $150 ($100 of this is interest, $50 is principal)
Amount still owed after first repayment: $4,950 ($5,100 – $150 repayment = $4,950).
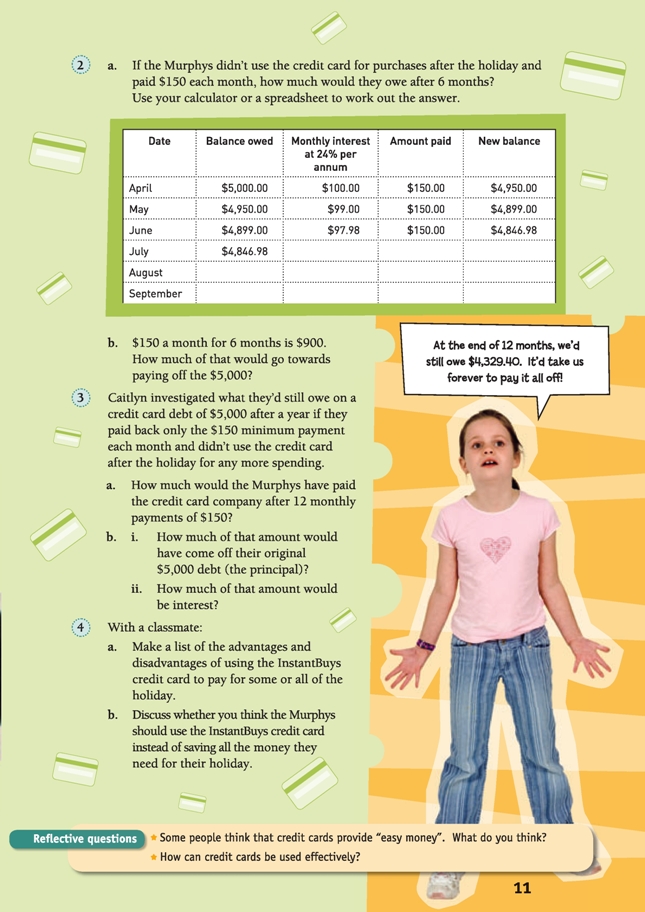
Question 2 is where the reality of paying back only the minimum amount required starts to hit home for the students as they work out the amount the Murphys would still owe after 6 months.
For this question, the students need to be able to work out 2 percent of numbers that are not as tidy as the initial $5,000, for example, 2 percent of $4,846.98. Brainstorm the range of strategies that the students could use for finding 2 percent of numbers, such as:
• finding 1 percent (by dividing by 100) and doubling it
• dividing by 50 (because [ ÷ 100] x 2 is the same as  ÷ 50)
• finding 1 tenth and dividing that by 5, or multiplying by 0.02 on the calculator (because 0.02 is equivalent to 2 percent, so 2 percent x ® is the same as 0.02 x ).
Encourage the students to make links between the different strategies by listing them all on the board and talking about how some are easier to do mentally and some are more efficient for a calculator.
A computer spreadsheet for question 3 is given below. (Note that if the table figures were calculated using a calculator, there would be some minor differences because the computer spreadsheet works with the entire unrounded numbers even though only two decimal places are shown. The cells are formatted for currency,
which involves rounding to two decimal places.) You could show it to the group on OHP or enlarged to A3, revealing it line by line to maximise the shock value of how little of the principal of the loan is paid off compared to the amount of interest paid month by month.

Although the Murphys have paid $1,800 over the year, $1,129.40 of this has been interest payments and they still owe $4,329.40. The interest payments will get lower each year because the balance will be lower, but this is conditional on the Murphys not borrowing against the card until they have paid it all off. You could discuss
with the students how they think the Murphys would cope with this. After all, they borrowed the money in the first place because they didn’t have the money they needed for the holiday. Now they’ve had the holiday, but they have to find $150 a month to pay off the cost of that holiday. Where is this $150 going to come from?
(You might go back to the bank statement on page 8 of the students’ book, which shows that the Murphys usually used up most of their income.)

The students could create a spreadsheet to calculate how long it would take the Murphys to repay the whole loan if they continued to repay only the $150 a month. They will need to use the “product” function to work out the interest charged each month, for example: “=PRODUCT(B2,0.02)”.
Use the “sum” function to work out the new balance owed on each line by creating a formula in cell E2 such as “=SUM(B2,C2,–D2)”. This formula tells the computer to take the amount owing in cell B2, add on the interest charge in cell C2, and deduct the repayment of $150 in cell D2 to work out the new balance.
The computer data for months 54–56 will look like this (spreadsheet works on unfounded numbers):

So the loan of $5,000 would cost the Murphys an extra $3,322.09 and take them 56 months (over 4 years!) to pay off – and during that time, they would have $150 a month less to spend on other things than they had before their holiday.
Extension
Financial understanding
As an extension, you could work through the following with your more able students:
When you have a mortgage from the bank (a really big loan that many people get so that they can buy a house or business), the interest is usually calculated daily rather than monthly, like the InstantBuys credit card. If the InstantBuys Credit Card Company decided to calculate their interest daily instead of monthly, would the Murphys end up repaying more or less?
(More, because the interest would keep compounding, and interest would be charged on interest more often.)
The interest charged on a mortgage might be 7.75 percent, while that on a credit card might be 19.65 percent. (The students could research actual amounts.) Why do you think there is such a difference in the interest charged? (Answers will vary but may include the fact that a mortgage is for an actual building or property, which can be
sold by the bank to recoup their money if necessary, whereas a credit card could be used for any purchases, including holiday expenses – there may be nothing to sell if the person hasn’t the money to pay the amount owing.)
Some students, particularly proportional thinkers working at stage 7, might be ready to explore the concept of compound interest and the effects of inflation on prices. Book 8: Teaching Number Sense and Algebraic Thinking, Inflation, page 45, introduces the compounding effect of inflation on prices.
There are online loan calculators that work out compound interest for mortgage loans. Get the students to explore the impact on the length of the loan and the total amount of interest paid if higher repayments are made or if one-off repayments of $1,000
are made each year. For example, say: The Consumer’s Institute of New Zealand advise that “Giving up a $3 treat (like a cappuccino) a week can save you thousands on your mortgage.” What would happen if the Murphys were able to repay just $12 extra a month on their loan?
The Retirement Commission asks questions such as “What would you do if you got an unexpected $1,000 given to you?” What would happen if the Murphys put that $1,000 into paying off some of their loan?

Social Sciences Links
Achievement objective:
• Understand how people make decisions about access to and use of resources (Social Studies, level 3)
Students could interview a budgeting adviser from the local Community Advice Bureau about ideas for managing their own pocket money effectively and what they can do now that will help them to avoid getting into difficulties when they get older and have access to more money.
They could do a social inquiry with the school principal and board of trustees about costs at school or special projects such as building a school hall or a gymnasium.

Other Cross-curricular Links
English achievement objectives:
• Purposes and audiences: Show a developing understanding of how to shape texts for different purposes and audiences (Speaking, Writing, and Presenting, level 3)
Students could pretend to be Nana and Grandad in Brisbane and write to the Murphys to persuade them to use/not to use the InstantBuys credit card to fund the holiday.
• Processes and strategies: Integrate sources of information, processes, and strategies with developing confidence to identify, form, and express ideas (Speaking, Writing, and Presenting, level 3)
Students could collect examples of advertisements for easy finance and analyse which features of the advertisements are designed to “hook” the reader or viewer. How many of the advertisements make the financial impact of the loan really clear? Get the students to re-present one of the advertisements in the same style but making the financial consequences of the loan the main aspect that stands out instead. For example, “No-fuss, no-hassle electronic equipment loans! With us, you can still be paying off your stereo long after the technology is out of date! 3 years interest free, but after that, you have to pay monthly for another 5 years, and no! you can’t pay your loan off early with a lump sum because we want the compound interest and compulsory insurance you’re going to have to pay!” 

Answers to Activities

1. a. Interest can be looked at in two ways:
interest you pay and interest you get. One possible definition: Interest is the amount that you have to pay for using someone else’s or the bank’s money or the amount that you earn by lending someone else or the bank your money.
b. Yes, Oscar is right. 24% per year ÷ 12 months = 2% per month (as long as the 24% per annum is calculated monthly, as in this case, not daily or just at the end of the year, because then the effects of compound interest would make the amount of interest slightly different in each case.)
c. 34 months, with the final payment being $50. ($5,000 ÷ $150)
d. $100. (For example, for 24% per annum, $5,000 x 0.24 ÷ 12 = $100; there are various ways to work out 2% per month.)
e. $4,950. ($5,000 original loan + $100 interest – $150 minimum payment; so they’d have paid only $50 off the loan.)
2. a. The Murphys would owe $4,684.60 after 6 months (based on spreadsheet calculations.

b. $315.40. (The remaining $584.60 would be interest: $900 – $584.60 = $315.40)
3. a. $1,800. (12 x $150 = $1,800)
b. Based on a computer spreadsheet:
i. $670.60 (a calculator would give an answer of $670.59). ($5,000 – $4,329.40 = $670.60)
ii. $1,129.40. ($1,800 – $670.60 = $1,129.40; a spreadsheet sum formula would add all the interest amounts together to get $1,129.40)
4. a. Answers will vary. Ideas could include: Advantages: they would be able to have their holiday without having to save for it beforehand, so they could go sooner if they wanted to; they could still earn and save money for the holiday, but they could then do extra or more expensive activities during the holiday.
Disadvantages: they would end up having to pay a lot more for their holiday because they would have to pay interest on their loan; it would be hard to remain motivated to work hard to earn money and cut costs to pay back the loan once they’d already been on the holiday and didn’t have it to look forward to; the credit card might entice them to spend more than they could afford because the credit card money would be readily available.
b. Answers will vary. The main problem would be the disadvantages listed in question 4a.
Reflective questions
• Answers will vary. It may seem “easy money” at first, but once it is spent and the maximum limit reached, it often becomes a huge debt that people never manage to get on top of, especially if most of the repayments are interest. Some people pay off the minimum due every month (which is mostly interest) and then spend that amount or more using the card, so the loan balance never goes down or slowly creeps up to the maximum limit.
• Credit cards can provide a way out in an emergency. You can also organise with the bank to pay your full balance automatically at the end of every month. In most cases, this means that no interest is charged. It also means that you think twice before you use the card because you need to have the money in the bank to cover the monthly balance. (If not, you end up paying penaltieas as well as interest.)
Used in this way, you can take advantage of the points offers that go with most credit cards but not let the debt become more than you can handle in a given month.