This is a level 4 number link activity from the Figure It Out series. It relates to Stage 7 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (519 KB)
find fractions, decimals, percentages of a whole number
know equivalent fractions, decimals and percentages
FIO, Link, Number, Book Three, Conversion Cousins - Part 2
For question 1, the students need to be able to find a fraction, a decimal, and a percentage of a whole number to complete the table and find the number of muffins each family ordered.
There are several ways to find the number of muffins. The students can choose whether to use fractions, (1/4 of 60), percentages (25% of 60), or decimals (0.25 of 60).
The following examples show how the students could approach solving these problems.
Example 1: What is 25% of 60?
The student might know that 50% is 1/2 or 0.5. Therefore 50% of 60 is 30, the same as half of 60. Also, half of 50% is 25%, so 25% of 60 is half of 30, that is, 15. In this example, the students use their knowledge of doubles and halves.
Example 2: What is 1/10 of 60?
The students might know that to find 1/10 of any number, you divide the number by 10. So 1/10 of 60 is the same as sharing 60 evenly between 10 groups, 60 ÷ 10, or 10 x = 60.
This might be a good time to ask the students to look for a short cut for finding 10% of any number. If they can figure it out for themselves, they are much more likely to understand it, remember it, and use it. Reinforce this by getting them to look for a short cut to help them find the answers to calculations such as: 10% of 50, 10% of 90, 10% of 120, 10% of 470, 10% of 2 360, and 10% of 10. Don’t forget to include numbers that involve decimals, such as 10% of 8, 10% of 12, 10% of 56.4, 10% of 4.70, 10% of 0.2, and 10% of 12.34.
Example 3: What is 1/3 of 60?
The students might know that 1/3 + 1/3 + 1/3 = 1 (or a whole or all of it). Following on from this, the whole, or 60, is divided up into three equal parts. Therefore we are looking for + + = 60. 20 + 20 + 20 = 60, so 1/3 of 60 is 20. So if 1/3 of 60 is 20, 2/3 of 60 is 40 (two lots of 20), 3/3 of 60 is 60 (three lots of 20),
4/3 of 60 is 80 (four lots of 20), and so on.
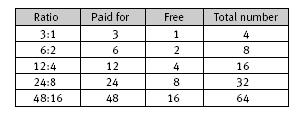
Question 2 will help the students to see and understand the connection between fractions and ratios. The problem can be represented and worked out as a ratio or as a fraction. In the ratio approach, 3:1 means that for every three muffins, one is free. This gives four in total, three paid for and one free. If six muffins are paid for, then a further two are free, a ratio of 6:2, which is equivalent to 3:1. If 12 muffins are paid for, then four more are free, a ratio of 12:4, which is equivalent to 3:1 and 6:2. This method of doubling is a good way to help the students to see the equivalent nature of some ratios. However, in this particular case, doubling does not lead to the required answer of 60 muffins, so the students need to do some further thinking. A table
such as the one below clearly shows the relationships and how they lead to too many muffins.
If you subtract one group of four muffins (three paid for and one free), you get to the desired total number, 60. 48 – 3 = 45 and 16 – 1 = 15, so 45:15 is the equivalent ratio with a total of 60. So if you pay for 45 muffins, you get 15 free.
Another way of thinking is to see how many groups of four are in the 60 muffins: 60 ÷ 4 = , x 4 = 60, or “If 60 is divided into groups of four, how many groups of four would there be?” There are 15 groups of four in 60, therefore 15 are free (one out of each group of four) and there are 45 to be paid for (three out of every group of four, and there are 15 groups, so 15 x 4 = 45 + 15).
In terms of the special offer, you could discuss with the students how many muffins the cousins would have paid for if they had filled each family’s initial requests (47).
Answers to Activity
1.
b. Five extra muffins
c. 15
2. 45 muffins
3. Answers will be similar to:
Fergus Fraction: “We got 1/4 off.”
Percy Percentage: “We got a 25% discount.”
Dewey Decimal: “We got 0.25 off.”