In this unit students explore different ways to communicate and explain adding numbers within ten and beyond. The representations included are number lines, set diagrams, animal strips and tens frames.
- Draw representations to show simple addition equations.
- Write an equation/number sentence to match their representation.
In this unit students are introduced to different ways to represent the addition of single digit numbers using sentences, equations and number lines. Students will be able to communicate their thinking using the representations.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. The difficulty of tasks can be varied in many ways including:
- adjusting the size of numbers used as appropriate
- varying the location of the unknown in the equation, result, change, or start
- using digital tools such as interactive tens frames and number lines created on a PowerPoint, or online tens frame tools, to model concepts. Search for “tens frame animations” to find a variety of these
- encouraging students to work collaboratively.
The contexts for this unit are a tens frame waka and native animals. The materials can be adapted to suit cultural knowledge and interests of your students. Using physical items that have significance to your students might be more engaging than using standard mathematical equipment. For example, if you have a big set of shells or stones for environmental studies you might use those shells as the materials for session 1. You might create ‘story shells’ that are appropriate to your students, such as hatchlings in a nest, baked goods in a tray, whanau members in whare, or people at a feast.
Session 1
In this session students are introduced to using a diagram or picture to communicate an addition equation. You may need to adjust the numbers used in the lesson in response to the knowledge of your students.
- Place 5 blue counters in a tens frame. The tens frame will support subitising (instant recognition of number in a set)
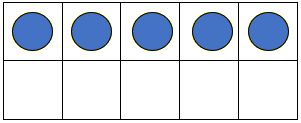
How many kaihoe/rowers are in the waka? Place 2 red counters in the tens frame and ask:
How many kaihoe/rowers are in the waka now?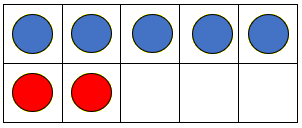
Students may count from one, i.e. 1, 2, 3, 4, 5, 6, 7.
Some students will be able to count on from the five i.e. 5... 6, 7.
Using two different colours will help encourage students to count on and support subitising (recognising 7 counters instantly).- Use another tens frame and place 5 blue counters in it.
How many kaihoe/rowers are in this waka?
Count with me as I add more kaihoe/rowers. - Add 3 counters and count as each counter is added "6","7","8".
How many kaihoe are in the waka now?
How many red counters did we put in? - Introduce the idea of recording what the diagram shows. Tell the students you are going to write the number sentence.
How many blue counters are there? (Write 5 in blue.)
And how many red counters are there? (Write 3 in red)
5 and 3 makes how many counters?
Record the equation 5 + 3 = 8.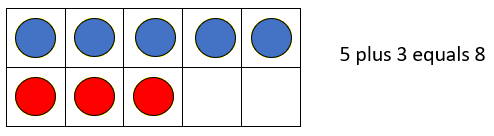
- Use Copymaster 1 as an open story shell to develop addition equations with numbers to ten in the waka context. Work with the students to draw tens frame diagrams. Use coloured pens to draw circles instead of using counters (or use coloured round stickers). Use the coloured pens to write the number sentence beside the set diagram. Number sentences can focus on facts to five or facts to ten depending on the students’ knowledge.
- Students can work in pairs or as individuals to practise using the waka tens frame diagram.
Session 2
In this session students continue to use tens frames to represent addition equations. They work on simple “change unknown” problems (e.g. 8 + □ = 10) in this lesson. You need a set of tens frames with dots. These can be made using the Copymaster.
- Remind students about the waka that holds 10 kaihoe/rowers.
Show students the waka model. How many kaihoe can get in the waka? How do you know?
Some students may recognise that 5 + 5 = 10. Show the students a tens frame waka with 6 kaihoe. For example:
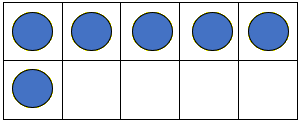
How many kaihoe are in the waka?
The waka needs a full crew. How many more kaihoe do we need?Students may be able to image 4 more dots and then count all the dots, or they may need you draw the 4 dots before they can count all the dots. Consider providing physical materials (e.g. counters) for those who need it.
- To encourage students to use counting on strategies, use a coloured pen to draw 4 more dots or add 4 more counters. Count with the students as extra kaihoe is added "7", "8", "9", "10".
- Write beside the tens frame the number sentence 6 and 4 makes 10, and record the equation 6 + 4 = 10.
- Make copies of the tens frames and ask pairs or individual students to complete addition equations for stories you give them. You might use Copymaster 2 as the source of the problems. Encourage students to count on as they add the extra dots or counters. Students then write the number sentence. Use an empty box to represent the extra dots or counters that are added. For example:
4 + □ = 7
Session 3
In this session students are introduced to Animal strips as a way to communicate addition equations. The animals are native to Aotearoa/New Zealand.
- Show the students the animal strips.
How many animals are on the strip? - Students may be able to recognise the patterns and answer instantly, rather than counting each animal. Show the students the dotted line after the 5th animal of the longer strips. The aim is that they subitise the number of animals using 'five and' groupings (i.e. recognise how many animals there are without counting them).
- Show the students an animal strip.
How many animals are on the strip?
- Show the students another animal strip and ask the students:
How many animals are there altogether?
- Encourage the students to count on, i.e. "8", "9".
- Write under the animal strip the number sentence "7 and 2 makes 9” and the equations 7 + 2 = 9.
- Make copies of the animal strips and ask pairs or individual students to make their own addition equations. Encourage students to count on as they add the animals. Then ask the students to write the number sentence underneath. Be open to students using early part-whole strategies and encourage other students to make sense of the strategies. For example, a student might add 5 + 4 using 4 + 4 = 8 and adding one to the answer.
- To extend student use addends with sums above ten, e.g. 6 + 5 = 11 or 7 + 8 = 15.
Session 4
In this session students are introduced to the number line as a way to represent addition problems.
- Put 4 counters on a number strip (Number strips) as shown below. Add another three counters. As you model with the materials say:
"I am making a putiputi (woven harakeke flower). I pick 4 strips of harakeke. Then I pick another 3 strips of harakeke. How many strips of harakeke do I have?
Expect students to tell you that the total is 7.
Draw a number line above the number strip as shown below. Highlight that the numbers go at the end of the counters, not the middle as you might do when pointing to the counters.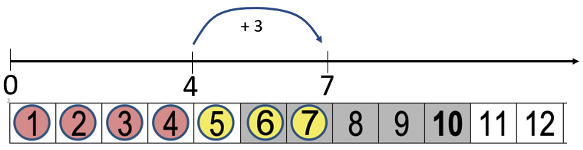
Remove the number strip and counters so only the number line remains.
What numbers have I written?
Why did I only write those numbers?
- Rehearse counting on with the students using only the empty number line. Say, "5", "6", "7".
- Record the number sentence 4 and 3 makes 7 and write the equation 4 + 3 = 7.
- Model the same process with other numbers such as 3 + 5 and 6 + 2. When students appear secure in moving between the number strip and number line representations, provide them with Copymaster 3 to work on in pairs. Some students may still require the number strip and counters to support their creation of the number line.
- Encourage the students to count on as they mark the jumps but be aware that students may use part-whole strategies as well, particularly based around doubles facts.
- After a suitable time, gather the class and discuss their answers.
Session 5
In this session students consolidate their use of representations. Provide them with an open people to solve, such as:
Mihi collected some paua in the morning and some more paua in the afternoon.
She collected 12 paua altogether. How many paua did she collect in the afternoon?
- Act out one possible solution using objects to represent the paua. Record the solution in various ways, such as:
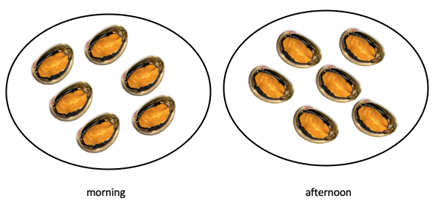
6 and 6 equals 12
6 + 6 = 12 Let students explore possible solutions. Encourage them to use as many representations as possible. Some students may need support with counters and numbers strips.
Can you find all the answers? How will you do that?
After a suitable time, record all the answers students found. Organise the equations systematically.
1 + 11 = 12
2 + 10 = 12
3 + 9 = 12
….
9 + 3 = 12
10 + 2 = 12
11 + 1 = 12Ask students what patterns they notice. Can they explain why the patterns occur?
- Investigate starting with the 6 + 6 scenario and explore moving paua from one time to the other.
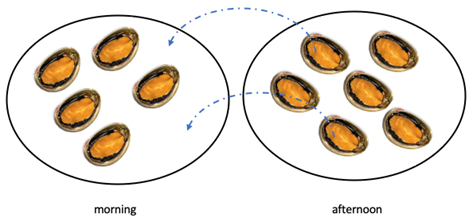
If time permits, use the same scenario to explore change-unknown addition problems.
Mihi collected 5 paua in the morning and some more paua in the afternoon.
She collected 9 paua altogether. How many paua did she collect in the afternoon?
Change unknown problems can be represented using a number line and equation.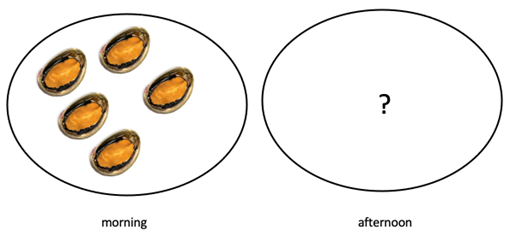

5 + ㅁ = 9For high achievers explore start-unknown addition problems such as:
Mihi has some paua. She gets 4 more paua. Now she has 10 paua.
How many did she have to start with?
Dear family and whānau,
This week in maths we have been using different representations to show addition number sentences. One way is using a set diagram, and then writing a number sentence (equation) to go with it:

6 + 4 = 10 or 6 and 4 equals 10
With your child draw some other set diagrams using 2 colours and record addition equations. This will help your child to understand addition.