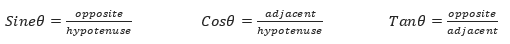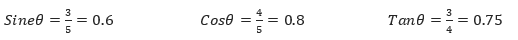In this unit, students will explore the use of trigonometry to find unknown sides and angles in right-angled triangles.
- Label right angled triangles with respect to a given angle.
- Use trigonometric ratios to calculate the length of opposite and adjacent sides, and the hypotenuse in right angled triangles.
- Use trigonometric ratios to calculate the size of angles in right angled triangles.
Maths skills required from other strands:
- Algebraic skills for solving equations.
- Rounding of decimals to a specified number of places.
- Enlargement factors.
This unit applies the concepts developed in the Level 5 unit Introducing Trigonometry.
Trigonometry can be traced as far back as ancient Egypt, and possibly Babylonia. The name comes from the Greek words for triangle (trigonon – three angles) and measure (metron). Hellenist mathematicians, around 500-300 BC, applied trigonometry to the location of stars and other celestial objects.
Therefore, the origins of trigonometry lay in practical measurement tasks of finding unknown sides and angles, using right angled triangles. Medieval Persian mathematicians developed trigonometry as a separate field of mathematics, and much later, in the late 1500’s, the trigonometric (or circular) functions were developed. Many real-life situations are modelled by trigonometric functions, such as sea levels as the tide changes, and day length as seasons change.
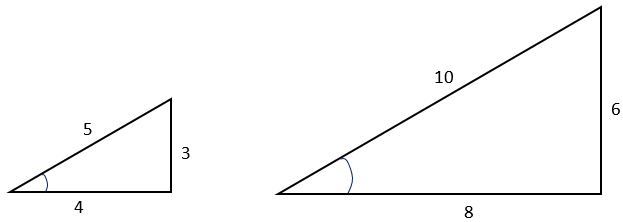
Trigonometry relies on the conservation of ratios between corresponding sides of similar right-angled triangles. Consider the case of two similar right-angled triangles. (3, 4, 5) and (6, 8, 10) are Pythagorean triples since 32 + 42 = 52 and 62 + 82 = 102. Therefore, the triangles are right-angled. The matching angles of both triangles are also equal (for example, the two angles marked). Less obvious is the proportional relationship between matching side lengths. The ratios 3/6, 4/8, and 5/10 are all 1/2 by division, which gives the scale factor mapping the larger triangle onto the smaller. The reciprocal ratios (6/3, 8/4, 10/5) are 2 which is the scale factor mapping the smaller triangle onto the larger.
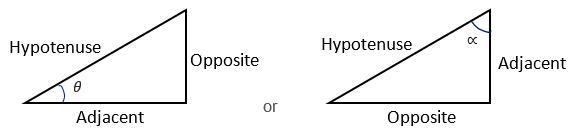
In fact, the matching side ratios are the same for any right-angled triangle that is similar to those two triangles. For example, the triangles (1½, 2, 2½) and (12, 16, 20) have the same side ratios. All four triangles also have the same matching angles. To formalise this idea the sides of any right-angled triangle are labelled with reference to one of the angles.
The opposite side is always ‘on the other side’ to the angle and the adjacent side is always ‘next to’ the angle. The hypotenuse is always the longest side.
The trigonometric ratios sine, cosine and tangent are the invariant side ratios for any right-angled triangle with the same angle they refer to.
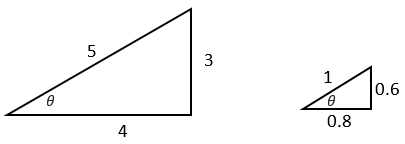
For example, in the (3, 4, 5) triangle, referring to as the angle in the left diagram:
Let’s imagine the (3, 4, 5) triangle enlarged by a factor of 0.2 or 2/5. That means that each side of the new triangle is one-fifth the original.
The unit triangle is useful for two reasons:
- It can be scaled up or down to match any triangle that is similar. Each side length is scaled by the same factor.
- It can be used to develop the relationship between angle and sine, cosine and tangent of that angle (The trigonometric functions).
To find θ, look up the angle with a sine of 0.6, a cosine of 0.8, and a tangent of 0.75. Any one of the three ratios will do. On a scientific calculator key in:
Sin-1(0.6) = 36.87◦ (2 dp) Cos-1(0.8) = 36.87° Tan-1(0.75) = 36.87°
This unit may take longer than one week. Introducing trigonometry through scale diagrams mimics historical development which may help students to appreciate the sophistication of using trigonometric ratios to find unknown lengths and angles.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
- modelling the labelling of right angled triangles, the use of ratios when calculating the length of the sides of a triangle, and the use of trigonometric ratios when calculating the size of angles in triangles
- grouping students flexibly to encourage peer learning, scaffolding, extension, and the sharing and questioning of ideas
- applying gradual release of responsibility to scaffold students towards working independently
- roaming and providing support in response to students' demonstrated needs
- providing frequent opportunities for students to share their thinking and strategies, ask questions, collaborate, and clarify in a range of whole-class, small-group, peer-peer, and teacher-student settings.
Te reo Māori kupu such as koki hāngai (right angle), ōwehenga (ratio), and pākoki (trigonometry) could be introduced in this unit and used throughout other mathematical learning.
- PowerPoint One
- Copymasters One, Two, Three and Four (some preparation of cards required)
- Protractors
- Rulers
- Scientific or graphics calculators
- Clinometers (see Trigonometric applications outside the classroom for instructions to make these instruments)
Getting Started
- In this session students examine whether, or not, it is justified to claim Dunedin’s Baldwin Street as the steepest street in the world. Currently, residents of a Welsh town are asserting that they have a steeper incline. You will find material about Baldwin Street online, including the famous Jaffa rolling event held each year until 2017.
- Work through the problems on PowerPoint One to refresh students’ understanding of trigonometric ratios as relationships between the sides of similar right-angled triangles.
- Provide students with Copymaster One which looks at alternate claims for title of steepest street. Students might work individually or in pairs. Look for students to:
- Recognise which trigonometric ratio is required for each situation
- Apply sound algebraic techniques for finding the unknowns, particularly applying inverse operations
- Express their answers to a suitable degree of accuracy with appropriate units.
Exploring
Give students, working in pairs, a set of matching activities (Copymaster Two). There are seven matching sets that might be used as the main part of a lesson or progressively over several days. Students need to shuffle the cards then attempt to:
- Match the story (word) cards to the diagram/equation cards
- Place the pairs of cards in the correct order for how the problem is solved.
Alternatively, you can delete parts of the sheet and the students can be challenged to:
- Write symbols to match words
- Write words to match symbols
- Fill in gaps in the words and symbols.
- Give students, working in groups of about 5, a cooperative logic problem to solve (Copymaster Three). There are seven problem sets so they can be used as the body of a lesson or as smaller tasks over several days:
- Each person in the group is given one clue card.
- Each person reads out their clue to the rest of the group. (Some problems may have unnecessary information mixed in with facts).
- The group then works on solving the problem cooperatively.
- The solution should be checked by reading the clues again to see that all conditions are satisfied.
If you choose to introduce Copymaster Three as a set of smaller tasks to be explored over a few days, consider using the time to also address specific, demonstrated learning needs with small groups of students (perhaps those you identified in session 1).
Reflection
Practical problem-solving activities
The students use their trigonometric ability to solve practical problems:
- Find a tall tree in the school grounds. Can the tree be felled safely if it gets diseased?
- Look at the disability access ramps at your school. Do the ramps comply with regulations you find on the internet?
- Try the problems on Copymaster Four. The tasks involve visualising the folding of nets and using trigonometry to predict heights and angles. Students also design nets to create solids with given specifications.
- Create a real-world problem for a partner to solve. The problem must require your partner to use one of the trigonometric ratios (sine, cosine or tangent). With your class, discuss a shared context (perhaps that relates to current learning from another curriculum area, to a local event or situation of interest, or to students' interests) that could be used as a base from which these problems can be developed.
Dear families and whānau,
Recently we have been exploring how to use trigonometry to find unknown sides and angles in right-angled triangles. Ask your child to share their learning with you.