Suspended Thought

In this activity, students carry out a practical experiment to investigate aspects of the mathematics of the curves found in suspension bridges.
The students model the behaviour of the cable of a suspension bridge and measure the “sag” at a number of points spaced along the curve. They use their results to estimate the length of the suspender cables needed for a real bridge.
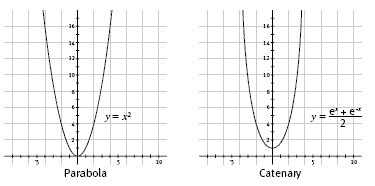
Over the years, many famous mathematicians have contributed to our understanding of the “chain-curves” formed when chains, ropes, or cables hang freely from their ends. Galilieo Gallilei (1564–1642) claimed wrongly that the curve is a parabola, rather like an upside-down version of the curve associated with a path of a ball thrown from one person to another. In 1691, mathematicians Gottfried Wilhelm von Leibniz (1646–1716), Christian Huygens (1629–1695), and Johann Bernouilli (1667–1748) found the equation of the chain curve that they named a catenary, from the Latin word for chain. Graphs of a parabola and a catenary are shown on the following page so that they can be compared.

Notice the differences between the two shapes. The more rounded catenary is due to the influence of gravity on each point of the curve and the tension in the chain, rope, or cable used for the catenary. The basic equation for the catenary is:

 (The students are not expected to use this sort of algebraic equation
at this stage.)
In this equation, e represents the constant value 2.718 281 828 …, known as “exponential e”. Here it is expressed to 9 decimal places but, in fact, it is an irrational number (a non-terminating, non-recurring decimal, like π [pi]). It pops up regularly in the mathematics associated with naturally occurring situations, especially in engineering. While the catenary in this activity relates to suspension bridges, the same ideas can also be applied to arches. The catenary arch is the arch that makes the best possible use of gravity to support itself.
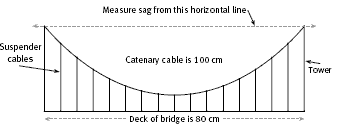
The cable catenaries that we see in suspension bridges appear more stretched than the catenary shown above. The curve below more accurately reflects the shape of the rope catenary that the students make with their model.

On their model, the students measure the sag at 5 centimetre intervals and then work out the lengths of the suspenders (vertical cables) measured from the catenary cable to the deck of the bridge.
The following diagram shows the measurements that the students should make.

The students use the results from their experimental work to try to predict the length of the suspenders for a real suspension bridge. The first investigation asks why the sides of a suspended rope or chain hang more steeply than the centre. This can be answered by imagining a chain with 200 links suspended over a gap. The two end links are each supporting the 99 links below them. The second-from-top links are supporting the 98 links below them, and so on. But the two links at the bottom are supporting nothing; they are simply “hanging on”. The links closer to the top of the sides are supporting the greatest mass, so the effect of gravity is felt most strongly by them, hence their more vertical tendency.
The second investigation invites students to find out about the Golden Gate Bridge. Built in 1937, this is the most famous of all suspension bridges, and it is still remarkable for its size, its engineering, and its beauty. Many consider that it is one of the top 10 engineering triumphs of the twentieth century. The facts about its
construction and the materials that went into its making should interest students. Good websites with information and photos are easily found. 

A third investigation would be to look into the advantages that suspension bridges have over swing bridges.
Three significant advantages are:

• they can span much greater gaps
• they can carry much greater loads
• they can have flat decks.

Answers to Activity

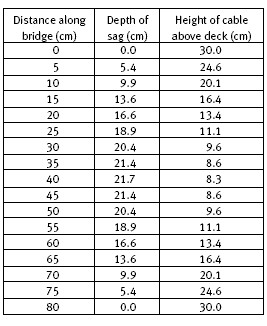
1. a.–c. Practical activity. The results come from actual measurements, so they will vary. A possible set of results is shown in the table below.

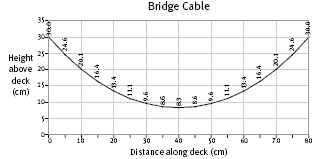
2. The shape of the catenary based on the measurements above is shown below.

3. Once the height of the towers is decided, the length of each vertical suspender cable is the tower height minus the depth of sag at that point. The bridge in this activity has towers that are 30 metres high. In each case, the depth of sag is subtracted from 30, as in the last column of the table in question 1. An engineer could use a graph like this by converting each y co-ordinate to metres. (The y co-ordinates
are the values in the last column of the table.)
4. As the length of the cable increases, so does the depth of sag. Also, the sides of the curve become steeper.
Investigation
Results will vary.
The sides of a suspended rope or chain hang more steeply than the centre because the links closer to the ends are supporting the greatest mass, so the effect of
gravity is felt most strongly by them.