In this unit students explore the different situation types to which multiplication can be applied. Particularly, they engage with rate, comparison and array problems.
- Pose different types of word problems.
- Explain their mathematical thinking in solving problems.
- Use a variety of equipment to model their solutions.
The basic concept of multiplication is an important one because of its practicality (how much do 4 ice creams cost at $2 each?) and efficiency (it is quicker to determine 4 x 2 than to calculate 2 + 2 + 2 + 2). Multiplication is used in many different situations. In this unit, students think about multiplication as a short way to find the result of repeated addition of equal sets. They do so by solving rate problems, comparison problems and array problems.
A rate problem involves a statement of "so many of one quantity for so many of another quantity". All multiplication situations contain some form of rate but at this level, the problems are usually about equal sets or measurement. For example:
“Lena buys six bags of biscuits. Each bag contains four biscuits. How many biscuits does she buy altogether?”
This is an equal sets problem that contains the rate "four biscuits for every bag". A measurement rate problem is usually something like this:
“Hone’s kumara plant grows five centimetres each week after it sprouts. How long will his plant be after six weeks?”
The rate in Hone’s problem is “five centimetres for every week". Comparison problems involve the relationship between two quantities, for example:
“Min’s apartment block has three floors. Anshul’s block has 12 floors. How much taller is Anshul’s block than Min’s?”
An additive answer is 12 – 3 = 9 floors. A multiplicative answer is 4 x 3 =12 so Anshul’s block is four times higher than Min’s. An array is a structure of rows and columns. For example, this chocolate block has two rows of five pieces (2 x 5 or 5 x 2).
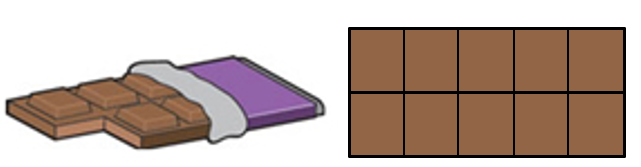
Array problems can help students to see the commutative property of multiplication, for example, that 5 x 2 = 2 x 5. In other words, the order of the factors does not affect the product (answer) in multiplication.
As well as thinking about multiplication in a variety of situations, students are encouraged to use a variety of materials to solve the problems. Using a variety of materials can help students see the multiplicative structure that is common to a variety of problems and assist them to transfer their understanding to situations which are new to them.
This unit can be differentiated by varying the scaffolding provided to make the learning opportunities accessible to a range of learners. For example:
- accepting students’ use of counting strategies to solve multiplicative problems, as needed
- having students use materials or diagrams to support their thinking, as needed
- working in small groups with students who need additional support, solving problems together.
The contexts for this unit can be adapted to suit the interests and experiences of your students. Focus on familiar contexts which include multiplicative situations to appeal to students’ interests and experiences and encourage engagement. Examples may include:
- lines of students in kapa haka groups
- collecting bags of pipi or other shellfish
- crews of students racing in waka ama
- loaves of rēwana bread for a school or community event
- groups of people travelling in vans, cars or buses
- preparing bundles of harakeke for weaving.
- Interlocking cubes
- Threading beads
- Number track
- Graph paper
- Ten-sided dice (or normal dice)
- Copymaster 1
- Copymaster 2
- Copymaster 3
- PowerPoint 1
Getting Started
Introduce the session by asking the students to work through several equal group (set) problems first and then ask them to pose their own problems. For example:
- There are 8 cars. Each one can take 2 people on the school trip. How many people are there altogether?
- There are 6 bags of shellfish (kaimoana). Each bag contains 4 pipi. How many pipi are there altogether?
- There are 7 waka in the race. Each waka holds 3 students. How many students are in the race?
When writing these problems, consider what times tables your students are confident in applying to word problems. Also consider how students might benefit from working in pairs (tuakana-teina).
The students can represent these and similar ‘equal sets’ problems with:- towers of interlocking cubes
- threading beads
- jumps on the number line
- interlocking cubes on a number track
- drawing a picture to show the number of waka and the corresponding number of students.
Note: It is important to link the examples (where possible) to the structure of repeated addition of equivalent sets as multiplication. For example: 4 + 4 + 4 + 4 + 4 + 4 + 4 = 28 or 7 x 4 = 28. Discuss what the numbers 4, 7, and 28 refer to and what the operations symbols + and x refer to. The multiplication symbols can be thought of as meaning ‘of’. For example, 7 x 4 = 20 means seven sets of four.
- Now ask the students to make up word problems using the problem structure above with different answers. For example, “Write a multiplication problem with an answer of 24”.
Use several sets of ice-cream containers (all with the same number of items in them) with the contents of each covered except for one. Ask the students to write story problems for each example.
- What strategy do the students use to solve the problems?
- Do they try to count the contents of each ice-cream container by ones; that is, those that are visible and those that are concealed?
- Do they use skip counting, e.g. 3, 6, 9, …, or repeated addition, e.g. 3 + 3 = 6, 6 + 3 = 9, …?
- Do they apply multiplication facts, e.g. 5 x 3 = 15 so 6 x 3 = 18 (3 more)?
Be aware that students’ choice of strategy depends on the connection between the conditions of each problem and the number resources that they have available. Expect that the strategies used by individual students will vary.
Exploring
Over the next three days the students are exposed to a variety of different types of story problems. They are encouraged to model the problems using different equipment and explain their answers to others. They think about the most efficient ways of solving the problems. It is important that students are provided with opportunities to build up multiplication facts to 10 and then to 20. Some students may solve these problems without equipment, using the number knowledge they have available.
Rate problems
- On the first day, work through several measurement rate problems. Draw on the multiplicative strategies students used previoulsy, and model how to work out the answer when necessary. It is good if students notice that the situations are structurally similar to the ‘equal sets’ problems from the previous session. Measurement quantities, especially time, are more intangible than ‘bags of’ or ‘packets of’ in equal sets situations. Acting out problems can support students to see the common structure.
- Use these measurement rate situations:
[Name] can write their name in 10 seconds. How long does it take to write their name four times?
You might select a student to role play writing their name and use an analogue clock (less battery) and/or stacks of cubes to track the time in seconds
[Name] drinks four cups of water each day. How many cups does he/she drink in one week?
Use plastic cups to build up the equal sets of four cups that are involved in this problem. Use another material to track the number of days.
[Name] puts five pieces of harakeke into every bundle. How many pieces of harakeke does he/she need for eight bundles?
[Name] puts three spoons of Milo in each cup. How many spoons of Milo does he/she need for 10 cups?
These problems are more accessible than the time related tasks. Shirts can be cut out of paper and buttons represented by counters. Cups and plastic spoons can be used to model the Milo problem. Both quantities in each rate are tangible.
- Copymaster 1 has some rate problems for students to solve. The problems contain a mixture of tangible and intangible units.
The students can create similar types of problems with pictures and pose the problems to each other. Encourage them to explain their strategies to each other.
- After time solving the problems, gather the class.
Discuss what is the same about all the problems you have just worked on.
Do students express the idea of a rate as being a “for every” relationship?
Now ask the students to make up similar word problems and to pose their problems to each other. Encourage them to explain their answers to each other.
Multiplicative comparison
- On the second day of exploration use PowerPoint 1 to expose your students to comparison situations. The first preference of students may be to look for additive relationships. For example, here is a correct additive response to the question on Slide One.
How much taller is Jill’s apartment block than Jack’s apartment block?
S: Jill’s apartment block has 12 floors and Jack’s has four floors. Jill’s block is eight floors higher.
Students may not offer a ‘times as many’ multiplicative answer. If that occurs pose this problem:
Jill says that her apartment block is three times higher than Jack’s block. I wonder what she means?
- Slides Two and Three show the additive and multiplicative comparisons that can be made.
Look for students to note the inverse relationships:
S: Jack’s apartment block is eight floors less (shorter) than Jill’s.
S: Jack’s apartment block is one third of the height of Jill’s. - Work through the other slides of PowerPoint 1 looking to see if students identify the common structure of finding difference (additive) and finding the scale factor (multiplicative).
- Copymaster 2 contains many multiplicative comparison problems. Some problems are in the form where the relationship is required while others require application of a given scale factor. Students are also encouraged to write equations to represent the situations. Let the students solve the problems, with the support of materials like counters if they need it. After a suitable time, share the answers as a class.
Do your students:- Recognise the meaning of “times as many.”?
- Represent the situations correctly with materials?
- Identify the scale factor and the set to be scaled?
- Record the equations correctly?
Arrays
- On the third day of exploration work through several array problems based on situations in which there are equal groups. When modelling arrays, it may be helpful to talk about the lines across as ‘rows’ and the lines up and down as ‘columns’. Teams with the same number of members in each are often used during the school day.
Pose problems such as:
The students are lined up in 3 teams for sport. Each team has 6 members. How many students are there altogether?
Encourage the students to draw representations of problems like this using three rows (one for each team) and six columns (one for each team member). Alternatively, use the students as the objects in the problem. If students draw the situation as three columns of six it opens discussion of the commutative property since 6 x 3 = 3 x 6.
- Other problems you might use include:
- A tray of eggs has five rows and six columns. How many eggs are in the tray altogether?
- The kapa haka group is arranged in four rows of children. There are ten children in each row. How many children are there altogether?
- A chocolate block has six columns, with four pieces in each column. How many pieces are in the whole block?
- A tray of rēwana bread for the school whānau day has seven columns, with six loaves of rēwana bread in each column. How many loaves of rēwana bread can fit on the whole tray?
- The students can model these and other array problems with:
- pegboards: pegs on a pegboard can be used to illustrate arrays in multiplication.
For the problem above this could be talked about as 3 rows of 6 pegs or 3 sixes,
or 3 rows of 6, or 3 x 6 = 18
By turning the pegboard a quarter turn, the array still has a total of 18 pegs.
This could be talked about as 6 columns of 3 pegs or 3 rows of 6 pegs or 6 threes or 6 columns of 3 or 6 X 3 + 18. - interlocking cubes
- colouring grid paper
- diagrams.
- pegboards: pegs on a pegboard can be used to illustrate arrays in multiplication.
- Copymaster 3 contains some problems related to arrays. Encourage your students to record an equation for each array, to show how they found the total number of objects.
Reflecting
On the final day of the unit we play a game called 'Array Trap' in which the students use graph paper to plot arrays.
For this activity you will need:
- a sheet of graph paper for each player (at least 30 x 20 squares);
- 3 x ten-sided dice - each side has a different digit on it (you can use 3 x standard 1-6 dice, but the facts are limited)
- different coloured felt pens.
Players take turns to:
- Roll the dice and choose two numbers, for example 8 and 2;
- Mark out a rectangle of that size, for example 8 rows of 2, or 2 columns of 8; or a different pair of factors with the same area, for example, four columns of four.
- Write the multiplication basic fact in the rectangle, for example 8 x 2 = 16 or 2 x 8 = 16;
- Players take turns until one player is trapped. That is, they are unable to find space for the array they have rolled.
Discuss strategies for the game such as:
- placing large arrays near the edge to maximise the space available for more arrays
- renaming the factors so the array fits a given space.
Dear Family and Whānau,
At school this week we have been solving multiplication problems. Here is an example of one we have worked on:
There are 6 bags of shellfish (kaimoana). Each bag contains 4 pipi. How many pipi are there altogether?
At home this week I would like your child to make up two more multiplication problems for us to solve in maths.