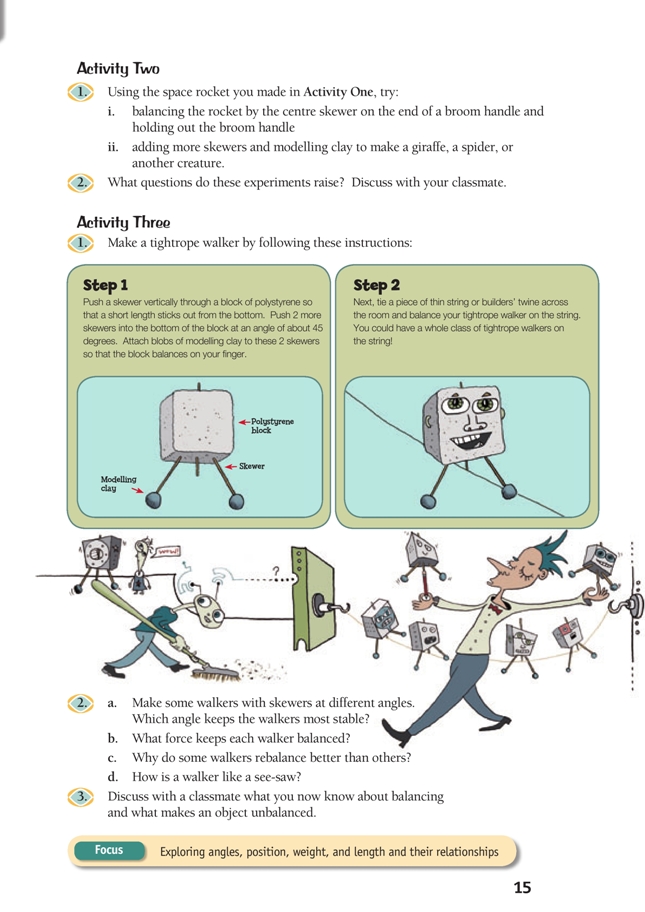
This is a level (2+ to 3+) mathematics in science contexts activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (1185 KB)
Students will:
- identify the relationship between the relative positions of weights, the centre of gravity of the system, and stability.
Students should discover that:
- the turning force (moment around the fulcrum) produced by gravity is a function of weight x horizontal distance from the fulcrum.
- as the arms get closer to horizontal, they effectively become longer:
- if a lever arm slopes down, lifting that side increases the horizontal length of the arm and therefore increases the turning force
- if a lever arm slopes up, lifting that side (making it more vertical) decreases the horizontal length of the arm distance and decreases the turning force.
thin string or builders' twine
modelling clay or other soft modelling material
wooden skewers
classmates
FIO, Forces, Levels 2+-3+, High Wire, pages 14 - 15
Background information; Activities One–Three
Teacher understanding
These background notes apply to all three activities. (Note that bamboo kebab sticks, which are cheap and easy to obtain, work well as skewers.) High Wire follows very closely from See-saw Antics (pages 10–11) and the notes for that activity should be read in conjunction with these.
The key question in Activity One is question 2c: “What is it that makes this object balance?” Although this activity introduces trigonometric concepts, students at this level only need to understand the effect of angle on vertical and horizontal distance.
The mathematics behind high-wire balancing is quite complex. To help the students, you don’t need to understand everything, but what you teach needs to be correct so that students don’t have false ideas that they carry through to higher levels. Use the following true or false list and notes to help you understand the ideas.
True:
- Any object will balance, no matter how strangely it is shaped.
- An object doesn’t have to be symmetrical* to balance – you can balance an object (such as a see-saw) that has a lot more weight on one side.
- You can balance a space rocket upside down – it’s just very, very diffi cult! (Although it is easier to balance on your feet, it is possible to balance on your head!) To balance, the fulcrum must be located at, directly above, or directly below the point where the turning forces of either side are equal.
- Balance is about turning forces, not overall forces. Even a heavy elephant can balance.
- Objects whose centre of gravity is above the fulcrum tend to be unstable. The turning forces are destabilising because tilting the object increases the weight on that side, which increases the turning force (weight x distance).
- The lower the centre of gravity is below the fulcrum, the more stable a structure will be.
False:
- Things with more weight are more stable.
- Force is the same no matter in what direction it’s exerted. (False because force is directional.)
Activity One
Preparation and points to note
A firmer material such as clay works better for the blobs than a softer material: the skewers and blobs are more likely to stay in place.
Gravity doesn’t “pull more” on any piece of the space rocket. Gravity accelerates every mass in the rocket the same way, although more mass will have more force because force = mass x acceleration of gravity. (Note that mass is the correct term here – weight is the force exerted on the mass.) Gravity is directional: it always pulls “down”. Turning force is also directional; it’s caused by forces perpendicular (at right angles) to the lever (in this case, the skewer). The closer a skewer is to horizontal, the larger the turning force will be for a given mass because the force of gravity is multiplied by a longer horizontal distance.
This seemingly simple activity about balance can lead deep into geometry and trigonometry. However, at this level, you only need to encourage the students’ intuition. Don’t let them get “bogged down” by complexities.
This activity and the one that follows provide opportunities for students to work with a diversity of classmates. By being actively involved in a group with a common interest and focus, they are developing skills that apply to the key competency participating and contributing.
Points of entry: Science and Mathematics
A space rocket with perfectly horizontal skewers (like Peter’s arms in the illustration) can balance but, like a see-saw, it is not very stable. Ask What happens when it tilts? Most students will know that if you push one side of a see-saw down, it will keep going down until it hits the ground (even though the turning forces are theoretically balanced and it should therefore be able to hold its position). Ask What’s really going on?
The turning force of a weight depends on its horizontal distance from the fulcrum; as the high side goes up, the weight moves further away from the fulcrum, and as the low side goes down, the weight gets closer to the fulcrum. A small weight a long way out can balance a larger weight closer in. As with a see-saw, as the high side moves up, its force increases; as the low side moves down, its force decreases.
One way of highlighting this is to attach strings to the bottom of the rocket body and to the blob on the end of each skewer. As the rocket tilts, the string on the low side approaches the centre; the string on the other blob moves further away.
Reinforce the idea that force has both size and direction. Gravity is always pulling “down”, so turning force is being applied vertically through the centres of the blobs at the end of each skewer.
Ask: What would happen if you angled the skewers upwards? Why is a space rocket like this difficult to balance? (The reason is that if one side tilts down, the horizontal distance of the weight from the fulcrum increases. The higher up the weight on the left, the less turning force it contributes.)
Encourage the students to use mathematical vocabulary to describe their space rockets and how they balance, for example, angle, slope, horizontal, vertical, distance.
Prompt students to make the connection between the skewers of the space rocket and the two ends of a see-saw. Introduce the idea of centre of gravity. The space rocket will balance when the centre of gravity is directly above or below the fulcrum, no matter at what angle the skewers are placed. Ask: If Peter (in the illustration) is balancing on one leg and sticks out the other leg, what does he do to stay balanced?
Answers
Activity One
1. Practical activity
2. a. Your space rocket will wobble if you move your finger, but if the centre of gravity is below the fulcrum, it will balance when the movement stops.
b. It can be pushed or moved quite a large distance about the fulcrum, but if the centre of gravity is below the fulcrum, it will balance when the movement stops.
c. The weights on the ends of the skewers work to restore balance. When the space rocket is disturbed, weights on one side lift up and weights on the other side go down. In this space rocket, the skewers are angled down, so the turning force on the high side will increase and the turning force on the low side will decrease. The weights on the high side (or those further out on a see-saw) move
further away from the centre of gravity and hence provide a bigger turning force that corrects the tilt.
3. a.–c. Investigation and discussion
Activity Two
Preparation and points to note
If you use kebab sticks as skewers, the students can easily cut these to length using scissors.
As with any investigation, try to deter the students from going straight into action. Encourage them to pose a hypothesis and plan their activity.
Points of entry: Mathematics
A 3-dimensional space rocket requires different spatial thinking compared with a 2-dimensional see-saw. Use this different thinking to explore the idea of X-Y-Z axes or 3-dimensional fi gures in general. Ask the students to describe the different movements of their space rocket and to draw diagrams or record the relative positions of the different weights using mathematical language. Ask: How would you describe your space rocket so that someone else could build an identical one? How is one space rocket different from another?
Challenge the students to achieve equality (balance) with unequal weights by varying the effective length of the skewers, not just through length but also through angle.
Points of entry: Science
If the students haven’t done so already, prompt them to think hard about the see-saw nature of the space rocket and how skewer angle affects horizontal distance of the weight from the fulcrum.
As noted in the support material for Activity One, gravity always pulls in the same direction, but changes in angle alter the amount of turning force produced by gravity. Encourage the students to predict which blob is providing the most turning force. In other words, before they attempt to balance a rocket by adjusting weight, length, and angle, ask them to plan their adjustment rather than use simple trial and error.
The centre of gravity is harder to identify when objects are not symmetrical or uniform. Push the students to locate the centre of gravity (see the diagram below) on their rockets by, for example, moving the fulcrum or hanging the rocket from strings attached at different points. Question them about the centre of gravity of a balanced see-saw where the fulcrum is not in the middle: What would that look like? How large a weight should be on each side? Challenge the students to locate the off-centre fulcrum for an irregularly-shaped space rocket.
When the students have tried out their ideas, encourage them to compare their thinking. Ask them to justify any new ideas to their classmates, especially if they have reached different conclusions.
Answers
Activity Two
1. Practical activity
2. Questions will vary. Possible questions may be:
- Why is one rocket more stable than another?
- How many legs can I add to my rocket and still have it balance?
- If I add a weight to one side, do I have to add an equal weight to the other side to make my rocket balance?
- How does the angle of the skewer and the position of the weight affect the way my space rocket balances?.
Activity Three
Preparation and points to note
Thin string such as a builder’s line works well for this activity. If students experience diffi culty positioning their tightrope walker on the thin string, a small blob of clay at the end of the central skewer will increase the contact area.
Make sure there is some variation between the tightrope walkers. The students could use coloured markers or glue to personalise their walkers.
Points of entry: Science and Mathematics
This activity reviews the ideas introduced in activities One and Two and asks students to demonstrate their understanding of turning force by applying their ideas to new shapes. Use this activity to reinforce understanding of turning force and centre of gravity or as an additional opportunity to ensure that all students can explain why some shapes are more stable than others.
Students can be the most effective teachers of other students. Try to identify which students have a good grasp of the principles in Activity One and pair them with students who are still struggling with the ideas.
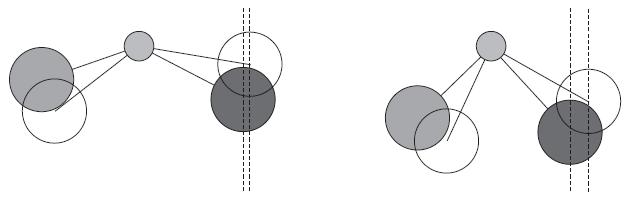
Ensure that the class as a whole comes to appropriate conclusions about the tightrope walkers. The most stable tightrope walker will have long legs at near vertical angles because a steeper leg gives a larger change in horizontal distance for the same amount of tilt, and hence a larger restorative turning force. In other words, the steep-legged walkers will return to a balanced state faster. For example, the tightrope walker on the left side of the diagram below has its grey and black legs at relatively shallow angles.
When it tilts, the centre of each weight moves only a small distance, as shown by the vertical lines going through the centre of the black weight and the clear circle representing the position of this weight after tilting. The tightrope walker on the right has its skewers for the grey and black weights at steeper angles. For the same amount of tilt, the centre of each weight moves a larger horizontal distance, represented by the gap between the dotted lines.
Answers
Activity Three
1. Practical activity
2. a. Practical activity. The most stable walker will be one with long skewers placed at an acute angle (less than 90°). (The more acute the angle, the lower the centre of gravity and hence the more stable. Similarly, the longer the skewers, the lower the centre of gravity and hence the more stable.)
b. Gravity keeps the walker balanced because it’s pulling down on each skewer. As a skewer becomes more horizontal (parallel to the ground), gravity causes more turning force because gravity is always pulling down vertically. When the walker tilts, the skewer closer to the horizontal provides more turning force, so it tends to return to vertical.
c. Very wide walkers will be less stable because there isn’t much difference in turning force between when the walker is balanced and when it is slightly tilted. Very tall, narrow walkers will be very stable because even a small tilt moves the skewers a long way sidewards, like someone sliding a long way further out on a see-saw. Because the skewer on the high side moves further from the fulcrum, that side goes back down, restoring the balance.
d. A walker is like a see-saw because the skewers of the walker are like the two ends of a see-saw and the centre of the tightrope is the fulcrum. The longer the skewers, the greater the force produced for a weight, just as a person on a see-saw produces more force by sitting close to the end.
3. Discussion will vary.