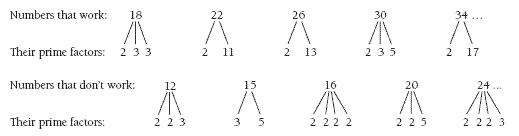This is a level 4 number activity from the Figure It Out series. It relates to Stage 7 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (440 KB)
find factors of numbers
generalise patterns for factors
Number Framework Links
Use this activity to develop your students’ knowledge of basic multiplication facts and their ability to identify factors. This leads to divisibility rules, which students need in order to become proportional thinkers. The activity is most suitable for students who are in transition from advanced additive (stage 6) to advanced multiplicative (stage 7) or higher.
FIO, Levels 3-4, Number Sense and Algebraic Thinking, Book Two, Factor Patterns, page 1
This activity explores patterns in the factors of the numbers 1 to 20. It builds on students’ recall of multiplication facts and helps them to develop their understanding of square numbers and square roots.
Question 1 asks the students to make a list of all the factors for the numbers from 1 to 20. They could draw this up as a table, or you could show them how to record the factors for each number as a set, using set brackets, a comma to separate items, and listing each factor only once. For example, the number sentences for 16 are 1 x 16 = 16, 2 x 8 = 16, and 4 x 4 = 16, and the factors for 16 are {1, 2, 4, 8, 16}. Once the students have listed the factors, encourage them to look for patterns. Ask: What is the name for numbers that have only 1 and the number itself as factors? (Prime
numbers have only two factors, 1 and the number itself. 1 is not considered to be a prime number because it only has one factor.)
Question 2 focuses on the pattern in numbers whose factors are half even numbers and half odd. (Students at the advanced additive stage will be able to describe the pattern [of half even, half odd factors] by adding on 4s or a combination of 4s and doubles and could still answer question 2d using this method.) For question 2b, the students should identify that, starting with 2, every fourth number fits the pattern. For question 2d, ask:
How can you use this information to find out if 102 is in the pattern? (Take 2 off 102 and divide the answer by 4. 102 – 2 = 100. 100 ÷ 4 = 25. So 102 is an “every fourth number” and must fit the pattern.)
Can you find a generalisation to see if any number fits the pattern? (Take 2 off the number and divide the answer by 4. If the result is a whole number [that is, it has no remainder], the original number will follow the pattern.)
The students may not realise that the pattern is linked to prime factorisation. They are not asked to explain this, but you may wish to explore this a bit with them. Drawing up a list of the prime factors of numbers that work and those that don’t work will help the students to recognise a pattern. For example:
The factors of numbers that work are 2 plus one or more odd primes. Numbers that don’t work have two 2s and an odd prime, two odd primes, three 2s and an odd prime, four 2s, and so on.
The pattern in question 3 is based on exponents of 2. The students should see that the pattern involves doubling, and they may be able to obtain the tenth number in the pattern by continuing the pattern (question 3d). Students who know about exponents should be able to describe the third number in the pattern, 8, as 2 x 2 x 2 or 23. Explain to them that the first number in a number sequence (or pattern) is known as the first term or term 1. This avoids over-using the word “number”. Then say: The second term in the pattern is 4 or 2 squared (22), and the third term is 8 or
2 cubed (23). Is there a short cut that you can use to find the value of any term in the pattern? (2place in pattern)
The students can use this information to find that the tenth number in the pattern or 210 is 1 024.
For question 4, the students will have already noticed that not all even numbers have an even number of factors. Even numbers that are also square numbers will have an odd number of factors because the square factor is only listed once. For example, the factors for 16 are 1, 2, 4, 8, and 16 because 4 x 4 contributes just one factor. The students could also represent square numbers using an array.
The students could investigate further square patterns, continue sequences, and make generalisations using the starters below:
12 = 1 x 1 = 1
22 = 2 x 2 = 4 = 1 + 3
32 = 3 x 3 = 9 = 1 + 3 + 5
and so on.
102 – 92 = 100 – 81 = 19 → 10 + 9 = 19
92 – 82 = 81 – 64 = 17 → 9 + 8 = 17
82 – 72 = 64 – 49 = 15 → 8 + 7 = 15
and so on.
A geometric explanation for these starters and another activity on the use of squares and exponents (powers) can be found in All Square, Algebra, Figure It Out, Levels 3–4, page 2. A spreadsheet activity on factors is The Great Factor Hunt, pages 2–3 of Number Sense and Algebraic Thinking: Book One, Figure It Out, Levels 3–4.
Answers to Activities
1.
2. a. 2, 6, 10, 14, 18
b. The numbers are going up in fours.
c. 22 and 26
d. Yes. The pattern starts at 2 and goes up in fours. 102 – 2 = 100, which is divisible by 4, so 102 is part of the pattern.
3. a. 2, 4, 8, 16
b. They are doubling (being multiplied by 2) each time. (Each number in the pattern is
2place in pattern. For example, 8 is the third number in the pattern.
22= 2 x 2 x 2)
c. 32. (16 x 2 or 25)
d. 1 024. (210 = 1 024)
4. a. 1, 4, 9, 16
b. They are square numbers. (The next one is 5 x 5 = 25.) The differences between the numbers form an odd number sequence: